��Ŀ����
����Ŀ����ͼ��ʾ��AOB�ǹ⻬ˮƽ�����BC�ǰ뾶ΪR�Ĺ⻬�� ![]() �̶�Բ������������ǡ��������B�㣮����ΪM��Сľ�龲ֹ��O�㣬һ������Ϊm���ӵ���ijһ���ٶ�ˮƽ��������Сľ���ڣ����������к�Сľ��һ���˶�����ǡ�ܵ���Բ���������ߵ�C��ľ����ӵ������Կ����ʵ㣩����
�̶�Բ������������ǡ��������B�㣮����ΪM��Сľ�龲ֹ��O�㣬һ������Ϊm���ӵ���ijһ���ٶ�ˮƽ��������Сľ���ڣ����������к�Сľ��һ���˶�����ǡ�ܵ���Բ���������ߵ�C��ľ����ӵ������Կ����ʵ㣩����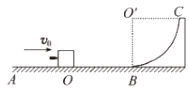
��1���ӵ�����ľ��ǰ���ٶȣ�
��2����ÿ��Сľ�鷵�ص�O���ֹͣ��O��ʱ����������ͬ���ӵ�����Сľ�飬���������У���9���ӵ�����Сľ���Сľ����Բ����������������߶�Ϊ���٣�
���𰸡�
��1���⣺���ݻ�е���غ㶨�ɵã�
![]() ��
��
��ã�v= ![]() ��
��
�ӵ�����ľ��Ĺ����У����ӵ���ľ����ɵ�ϵͳ�о����涨����Ϊ�������ݶ����غ�ã�
mv0=��M+m��v��
��ã� ![]() ��
��
���ӵ�����ľ��ǰ���ٶ�Ϊ ![]()
��2���⣺�ɶ����غ㶨�ɿ�֪����2��4��6�����ӵ�����ľ���ľ����ٶ�Ϊ0��
��1��3��5�����ӵ������ľ���˶�������9���ӵ�����ľ��ʱ�����ӵ����ٶȷ���Ϊ�������ɶ����غ㶨�ɵã�
mv0=��9m+M��v9��
��˺�ľ����Բ�����������߶�ΪH���ɻ�е���غ�ã�
![]()
�����ϸ�ʽ�ɵã�H= ![]() ��
��
��Сľ����Բ����������������߶�Ϊ ![]()
����������1���ɶ����غ㶨�����е���غ㶨�ɿ���������ٶȣ���2���ɶ����غ㶨�����е���غ㶨��������߶ȣ�
�����㾫����ͨ��������û�е���غ㼰�������Ͷ����غ㶨�ɣ�������ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ��䣻�����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��伴���Խ����⣮

 ��ѧ����ϵ�д�
��ѧ����ϵ�д�