题目内容
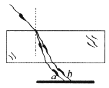
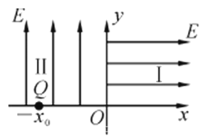
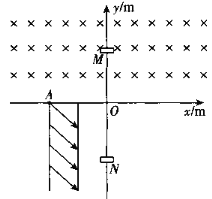
【题目】在光滑的水平面内存在如图所示直角坐标系,第一、二象限内有垂直纸面向里的匀强磁场,磁感应强度![]() .在第三象限
.在第三象限![]() 至
至![]() 间有斜向右下方与x轴夹角为45°的匀强电场,场强
间有斜向右下方与x轴夹角为45°的匀强电场,场强![]() .在y轴正、负半轴上的M点和N点各有一个极短的平板,由A点(-2m,0)静止释放一个质量为m=0.01kg,电量
.在y轴正、负半轴上的M点和N点各有一个极短的平板,由A点(-2m,0)静止释放一个质量为m=0.01kg,电量![]() 的小球,小球运动过程中会与两平板上表面发生完全弹性碰撞(碰撞时,小球在x轴方向速度不变,y轴方向速度大小不变,方向相反,碰撞时间不计),经过一段时间回到A点.求:
的小球,小球运动过程中会与两平板上表面发生完全弹性碰撞(碰撞时,小球在x轴方向速度不变,y轴方向速度大小不变,方向相反,碰撞时间不计),经过一段时间回到A点.求:
(1)小球射出电场的速度;
(2)平板M的坐标;
(3)小球从A点出发到返回至A点所经历的时间.
【答案】(1)2m/s (2) M(0,2m) (3) 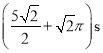
【解析】
(1)小球在电场中沿场强方向做匀加速直线运动,根据动能定理有:
![]()
又因为场强方向与水平方向夹角为45°,故
![]()
所以解得:
v=2m/s
(2)小球射出电场后做匀速直线运动,打到N板上,有几何关系可知N点的坐标为(0,-2m),击中N后由题意可知反弹以与水平方向成45°斜向上方匀速直线运动,进入磁场.小球进入磁场后的半径:
![]()
代入数据解得:
![]()
故小球在第一象限转半圆打到M点,故根据几何关系可得M点的坐标为(0,2),根据题意击中M后再在第二象限转半圆回到A点。小球的轨迹如图所示。
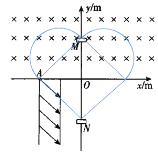
(3)由轨迹图可知,小球在电场中做加速运动的平均速度为:
![]()
时间为:
![]()
由几何关系可知做匀速直线运动的时间为:
![]()
而在磁场中做圆周运动恰好为一个完整圆周,故时间为:
![]()
所以总时间为:
![]()

练习册系列答案
相关题目