题目内容
如图甲所示，一质量为m=1.0kg的木块从倾角为α=37°、长度为L=3.2m的固定粗糙斜面顶端由静止开始运动，同时木块受水平向左的风力作用，且水平风力与风速成正比，木块在斜面上下滑时的加速度a与风速v之间的关系如图乙所示．已知sin 37°=0.6，cos 37°=0.8，取重力加速度大小为g=10m/s2，请求解：（1）木块与斜面间的动摩擦因数
（2）风速v=3.0m/s时木块沿斜面下滑的时间t及木块所受水平风力F的大小．
分析：（1）根据风速为0时，物体下滑的加速度为4.0m/s2，根据牛顿第二定律求出木块与斜面间的动摩擦因数．
（2）根据a-v图线得出a与v的关系式，从而得出v=3m/s时的加速度，根据位移时间公式求出运动的时间，根据牛顿第二定律求出水平风力的大小．
（2）根据a-v图线得出a与v的关系式，从而得出v=3m/s时的加速度，根据位移时间公式求出运动的时间，根据牛顿第二定律求出水平风力的大小．
解答：解：（1）当风速为0时，物体下滑的加速度为4.0m/s2，
由牛顿定律得物体的加速度为：a=gsinα-μgcosα
解得：μ=0.25．
（2）由a-v图象可得，a=4-0.8v
当v=3m/s时，物体下滑的加速度为a=1.6m/s2．
由运动学公式得，L=
at2，解得t=2.0s
由牛顿第二定律得：mgsin37°-Fcos37°-μ（mgcos37°+Fsin37°）=ma
解得：F=2.5N
答：（1）木块与斜面间的动摩擦因数为0.25．
（2）风速v=3.0m/s时木块沿斜面下滑的时间t为2.0s，木块所受水平风力F的大小为2.5N．
由牛顿定律得物体的加速度为：a=gsinα-μgcosα
解得：μ=0.25．
（2）由a-v图象可得，a=4-0.8v
当v=3m/s时，物体下滑的加速度为a=1.6m/s2．
由运动学公式得，L=
| 1 |
| 2 |
由牛顿第二定律得：mgsin37°-Fcos37°-μ（mgcos37°+Fsin37°）=ma
解得：F=2.5N
答：（1）木块与斜面间的动摩擦因数为0.25．
（2）风速v=3.0m/s时木块沿斜面下滑的时间t为2.0s，木块所受水平风力F的大小为2.5N．
点评：解决本题的关键能够正确地受力分析，结合图线运用牛顿第二定律进行求解．
练习册系列答案
相关题目
（2011?上海模拟）如图甲所示，一质量为m=1kg的小物块静止在粗糙水平面上的A点，从t=0时刻开始，物体在受如图乙所示规律变化的水平力F作用下向右运动，第3s末物块运动到B点时速度刚好为零，第5s末物块刚好回到A点，已知物块与粗糙水平面间的动摩擦因数μ=0.2，则物体从A运动到B间的平均速度为
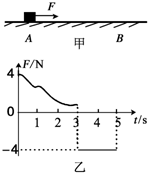如图甲所示，一质量为m=1kg的小物块静止在粗糙水平面上的A点，从t=0时刻开始，物体在受如图乙所示规律变化的水平力F作用下向右运动，第3s末物块运动到B点时速度刚好为零，第5s末物块刚好回到A点，已知物块与粗糙水平面间的动摩擦因数μ=0.2．（g取10m/s2）则