题目内容
【题目】边长为d的正方体透明介质置于真空中，其横截面ABCD如图所示。有两束平行光I、Ⅱ分别从上表面的A点和AB的中点沿与水平方向成30°角同时斜射入介质中，两种光在界面上折射后恰好相交于正方体底面的C点处。已知真空中光速为c，求：
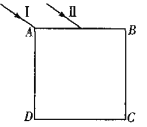
(1)介质对光I、Ⅱ的折射率；
(2)光I、Ⅱ到达C点的时间差。
【答案】（1）
（2）
【解析】
（1）画出光线Ⅰ、Ⅱ由空气射向介质中的光路图，结合几何关系求解折射角，根据
求解折射率；（2）由光线Ⅰ、Ⅱ在介质中的速度求解光I、Ⅱ到达C点的时间差。
（1）由题可知，光线Ⅰ、Ⅱ在空气中入射角为θ=600，做出光线Ⅰ、Ⅱ在介质中的光路图如图；
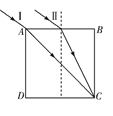
根据几何关系可知，光线Ⅰ在介质中的折射角为θ1=450，光线Ⅱ在介质中的折射角的正弦值为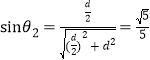
由折射定律：
解得
（2）由介质中光速：
可得光线Ⅰ、Ⅱ在介质中的速度分别为：
，
，
则有：
解得
练习册系列答案
相关题目
