题目内容
 如图所示,质量均为m的两个完全相同的小球A、B(可看成质点),带等量异种电荷,电量均为Q.通过绝缘轻弹簧相连接,弹簧的劲度系数为K,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场、场强为E,两小球A、B将由静止开始运动.则在以后的运动过程中,对两个小球和弹簧所组成的系统(设整个过程中不考虑两电荷之间的库仑力作用且弹簧不超过弹性限度),求:
如图所示,质量均为m的两个完全相同的小球A、B(可看成质点),带等量异种电荷,电量均为Q.通过绝缘轻弹簧相连接,弹簧的劲度系数为K,置于绝缘光滑的水平面上.当突然加一水平向右的匀强电场、场强为E,两小球A、B将由静止开始运动.则在以后的运动过程中,对两个小球和弹簧所组成的系统(设整个过程中不考虑两电荷之间的库仑力作用且弹簧不超过弹性限度),求:(1)小球速度最大时弹簧的形变量和系统电势能的改变量
(2)设小球最大速度大小为vm,求小球从静止释放到速度大小为vm过程中弹簧的弹力所做的功W.
分析:(1)分析小球的运动情况可知,电场力与弹簧的弹力平衡时,小球的速度最大.根据胡克定律求出小球速度最大时弹簧的形变量.由W=qEd求出电场力做功,即可求得电势能的变化量.
(2)根据动能定理,对小球列方程求解弹簧的弹力所做的功W.
(2)根据动能定理,对小球列方程求解弹簧的弹力所做的功W.
解答:解:(1)在水平方向上,两球都受电场力与弹簧的弹力,电场力先大于弹力,小球加速运动,后电场力小于弹力,小球减速运动,故当电场力与弹簧的弹力平衡时,小球的速度最大.
则有:QE=kx
则得:x=
此过程中,电场力做功为 W电=2QEx=2QE?
=
.
(2)对任一小球,从静止释放到速度大小为vm过程中,根据动能定理得:QEx+W′=
m
则得弹簧的弹力做功:W′=
m
-
故弹簧的弹力所做的功:W=2W′=2(
m
-
)
答:
(1)小球速度最大时弹簧的形变量为
,系统电势能的改变量为
.
(2)设小球最大速度大小为vm,小球从静止释放到速度大小为vm过程中弹簧的弹力所做的功W是2(
m
-
).
则有:QE=kx
则得:x=
| QE |
| k |
此过程中,电场力做功为 W电=2QEx=2QE?
| QE |
| k |
| 2Q2E2 |
| k |
(2)对任一小球,从静止释放到速度大小为vm过程中,根据动能定理得:QEx+W′=
| 1 |
| 2 |
| v | 2 m |
则得弹簧的弹力做功:W′=
| 1 |
| 2 |
| v | 2 m |
| Q2E2 |
| k |
故弹簧的弹力所做的功:W=2W′=2(
| 1 |
| 2 |
| v | 2 m |
| Q2E2 |
| k |
答:
(1)小球速度最大时弹簧的形变量为
| QE |
| k |
| 2Q2E2 |
| k |
(2)设小球最大速度大小为vm,小球从静止释放到速度大小为vm过程中弹簧的弹力所做的功W是2(
| 1 |
| 2 |
| v | 2 m |
| Q2E2 |
| k |
点评:本题关键要正确分析小球的运动情况,抓住电场力做功与电势能变化的关系、总功与动能变化的关系列式求解.

练习册系列答案
相关题目
 (2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( )
(2011?河西区二模)如图所示,质量均为m的A、B两球之间系着一根不计质量的弹簧,放在光滑的水平面上,A球紧靠竖直墙壁,今用水平力F将B球向左推压弹簧,平衡后,突然将F撤去,在这瞬间( ) 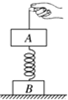 如图所示,质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连,开始时B放在地面上,A、B均处于静止状态,现通过细绳将A缓慢地向上拉起,当B刚要离开地面时,求A上升距离(假设弹簧一直在弹性限度内,重力加速度g已知)
如图所示,质量均为m的物体A、B通过一个劲度系数k的轻弹簧相连,开始时B放在地面上,A、B均处于静止状态,现通过细绳将A缓慢地向上拉起,当B刚要离开地面时,求A上升距离(假设弹簧一直在弹性限度内,重力加速度g已知)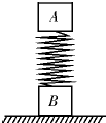 (2013?湖南模拟)如图所示,质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端,当A静止时弹簧的压缩量为l.现用一竖直向下的恒力F=3mg作用于A上,当A运动一段距离x,后撤去F,结果B刚好不离开水平面,则l:x的值为( )
(2013?湖南模拟)如图所示,质量均为m的A、B两物体分别固定在质量不计的轻弹簧的两端,当A静止时弹簧的压缩量为l.现用一竖直向下的恒力F=3mg作用于A上,当A运动一段距离x,后撤去F,结果B刚好不离开水平面,则l:x的值为( )