题目内容
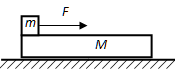
【题目】如图所示，水平传送带AB长2 m，以v=l m/s的速度匀速运动．质量均为4 kg的小物体P，Q与绕过定滑轮的轻绳相连，t=0时刻P在传送带A端以初速度v0=4 m/s向右运动，已知P与传送带间动摩擦因数为0.5，P在传送带上运动过程它与定滑轮间的绳始终水平。不计定滑轮质量和摩擦，绳不可伸长且有足够长度，最大静摩擦力近似等于滑动摩擦力，取g=l0 m/s2。求：
（1）t=0时刻小物体P的加速度大小和方向。
（2）小物体P滑离传送带时的速度。
【答案】（1）a1=7.5 m/s2 方向向左 （2）
m/s
【解析】（1）由于v0>v，所以P向右减速运动
对P：T+μmg=ma1①
对Q：mg–T=ma1②
a1=7.5 m/s2③
方向向左
（2）设经过时间t1速度与传送带速度相同，则
④
位移
⑤
由于最大静摩擦力
，所以此后P将继续向右减速
加速度：
m/s2⑥
当其速度减为0时，位移
⑦
可知P在速度未减为0时没有到达B端，此后P将反向向左加速从A端离开传送带
由：
⑧
得： m/s⑨
练习册系列答案
相关题目
