题目内容
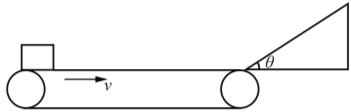
【题目】如图所示为上、下两端相距L=5 m、倾角α=30°、始终以v=3 m/s的速率顺时针转动的传送带(传送带始终绷紧)。将一物体放在传送带的上端由静止释放滑下,经过t=2 s到达下端。重力加速度g取10 m/s2,求:

(1)传送带与物体间的动摩擦因数多大?
(2)如果将传送带逆时针转动,速率至少多大时,物体从传送带上端由静止释放能最快地到达下端?
【答案】(1)μ=![]() (2)vm=8.66 m/s
(2)vm=8.66 m/s
【解析】(1)传送带顺时针转动,有题意得:
L=![]()
解得:a=2.5 m/s2
根据牛顿第二定律得:
Mgsin α–μmgcos α=ma
解得:μ=![]()
(2)如果传送带逆时针转动,要使物体从传送带上端由静止释放能最快地到达下端,则需要物体有沿传送带向下的最大加速度即所受摩擦力沿传送带向下,设此时传送带速度为vm,物体加速度为a'
由牛顿第二定律得mgsin α+Ff=ma′
而Ff=μmgcos α
根据位移速度公式得:vm2=2La'
解得:vm=8.66 m/s

练习册系列答案
相关题目