题目内容
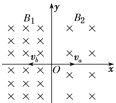
【题目】如图所示，在x轴的负方向，存在磁感应强度为B1，方向垂直于纸面向里的匀强磁场，在x轴的正方向，存在磁感应强度为B２，方向也垂直于纸面向里的匀强磁场，且B1∶B2＝3∶2。在原点O处同时发射两个质量分别为ma和mb的带电粒子，粒子a以速率va沿x轴正方向运动，粒子b以速率vb沿x轴负方向运动，已知粒子a带正电，粒子b带负电，电荷量相等，且两粒子的速率满足mava＝mbvb。若在此后的运动中，当粒子a第4次经过y轴(出发时经过y轴不算在内)时，恰与粒子b相遇。粒子重力不计。下列说法正确的是（ ）
A. 粒子a、b在磁场B1中的偏转半径之比为3∶2
B. 两粒子在y正半轴相遇
C. 粒子a、b相遇时的速度方向相同
D. 粒子a、b的质量之比为1∶5
【答案】BCD
【解析】
本题涉及到两个粒子分别在两个不同磁场中做匀速圆周运动问题，相遇问题既考虑到位移问题，又考虑到时间等时，比较复杂，所以要从简单情况出发，由题意a粒子逆时针旋转，b粒子顺时针旋转，由于两粒子的动量（m2va=m1vb）和电量相同，则半径之比就是磁感应强度的反比，所以在B1磁场中的半径小，则两粒子在两磁场旋转两个半周时，a粒子相对坐标原点上移，b粒子相对坐标原点下移，若b粒子在最初不相遇，则以后就不能相遇了。所以只考虑b粒子旋转半周就与a粒子相遇的情况。
由带电粒子在匀强磁场中做匀速圆周运动的半径公式
知道：
，所以选项A错误。由带电粒子在匀强磁场中做匀速圆周运动的半径公式r＝
知道，a粒子从O点出发沿x轴正方向射出向上逆时针转半周在y轴上上移2ra2，穿过y轴后逆时针向下转半周后下移2ra1，由于B2＜B1，则第二次经过y轴时在从标原点的上方（2ra2-2ra1）处，同理第四次经过y轴时在坐标原点上方2（2ra2-2ra1）处，所以由题意知选项B正确。从最短时间的情况进行考虑，显然是b粒子向上转半周后相遇的，a粒子第四次经过y轴时是向右方向，而b粒子转半周也是向右的方向，所以两者方向相同，所以选项C正确。根据周期公式
及题意，当两粒子在y轴上相遇时，时间上有：
Tb1＝Ta1+Ta2 即：
，结合B1：B2=3：2，得到：
，所以选项D正确。故选BCD。
