题目内容
【题目】如图所示为某种弹射装置的示意图，该装置由三部分组成，传送带左边是足够长的光滑水平面，一轻质弹簧左端固定，右端连接着质量M=6.0kg的物块A。装置的中间是水平传送带，它与左右两边的台面等高，并能平滑对接。传送带的皮带轮逆时针匀速转动，使传送带上表面以u=2.0m/s匀速运动。传送带的右边是一半径R=1.25m位于竖直平面内的光滑1/4圆弧轨道。质量m=2.0kg的物块B从1/4圆弧的最高处由静止释放。已知物块B与传送带之间的动摩擦因数μ=0.1，传送带两轴之间的距离l=4.5m。设物块A、B之间发生的是正对弹性碰撞，第一次碰撞前，物块A静止。取g=10m/s2。求：
（1）物块B滑到1/4圆弧的最低点C时对轨道的压力；
（2）物块B与物块A第一次碰撞后弹簧的最大弹性势能；
（3）如果物块A、B每次碰撞后，物块A再回到平衡位置时弹簧都会被立即锁定，而当它们再次碰撞前锁定被解除，求物块B经第一次与物块A碰撞后在传送带上运动的总时间。
【答案】（1）F1=60N，方向竖直向下（2）12J（3）8s
【解析】（1）设物块B沿光滑曲面下滑到水平位置时的速度大小为v0.由机械能守恒知
mgR＝
mv02得
=5 m/s
设物块B滑到1/4圆弧的最低点C时受到的支持力大小为F，
由牛顿第二定律得： 
解得：F=60N
由牛顿第三定律得：物块B滑到1/4圆弧的最低点C时受到的支持力大小为F1=60N，
方向竖直向下。
（2）设物块B在传送带上滑动过程中因受摩擦力所产生的加速度大小为a，则
μmg＝ma
设物块B通过传送带后运动速度大小为v，有v2-v02=-2al
联立解得v＝4 m/s
由于v>u＝2 m/s，所以v＝4m/s即为物块B与物块A第一次碰撞前的速度大小。
设物块A、B第一次碰撞后的速度分别为v2、v1，取向左为正方向，
由动量守恒定律和能量守恒定律得
mv＝mv1＋Mv2
mv2＝
mv12＋
Mv22 （（动量守恒、能量守恒）
解得v1＝
=-2m/s，v2=2m/s
弹簧具有的最大弹性势能等于物块M的初动能
EP=
Mv22=12J
（3）碰撞后物块B沿水平台面向右匀速运动。
设物块B在传送带上向右运动的最大位移为l′，
由动能定理得：－μmgl′=0－
mv12
得l′＝2m<4.5m
所以物块B不能通过传送带运动到右边的曲面上．当物块B在传送带上向右运动的速度为零后，将会沿传送带向左加速运动．可以判断，物块B运动到左边台面时的速度大小为
v1′＝2m/s，继而与物块A发生第二次碰撞．设第1次碰撞到第2次碰撞之间，物块B在传送带运动的时间为t1。
由动量定理得：μmgt1＝2mv1′
解得
设物块A、B第一次碰撞后的速度分别为v4、v3，取向左为正方向，由动量守恒定律和能量守恒定律得
mv1′＝mv3＋Mv4
mv1′2＝
mv32＋
Mv42
解得v3＝
=-1m/s
当物块B在传送带上向右运动的速度为零后，将会沿传送带向左加速运动．可以判断，物块B运动到左边台面时的速度大小为v3′＝1m/s，继而与物块发生第2次碰撞．则第2次碰撞到第3次碰撞之间，物块B在传送带运动的时间为t2。
由动量定理得：μmgt2＝2m v3
解得
同上计算可知
物块B与物块A第三次碰撞、第四次碰撞……第n次碰撞后物块B在传送带运动的时间为tn=
s, 构成无穷等比数列，公比q=
由无穷等比数列求和公式
可知，当n→∞时，有
物块B经第一次与物块A碰撞后在传送带运动的总时间为
t总=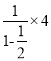
=8s
