��Ŀ����
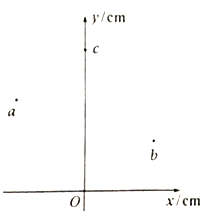
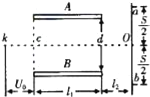
����Ŀ����ͼΪʾ�����IJ��ֹ��죬������е缫�������ϵط�����ӣ����ٶȲ��ƣ���������ѹΪUa�ļ��ٵ糡����С��C��ˮƽ������A��B�������������������䣬�峤Ϊl1������Ϊd�����Ӵ����������ӫ�����ϣ����������Ե�ľ���Ϊl2��A��B����䲻�ӵ�ѹʱ�����Ӵ��ڿ����������е�O�ϣ�����a��b���㵽O��ľ����Ϊ![]() ������A��B�������ϱ仯�ĵ�ѹ����ÿ������ͨ������ļ���ʱ���ڣ��糡ǿ�ȿ���Ϊ�㶨���䣬��Ҫ��t=0���������ĵ��Ӵ������ϵ�b�㣬Ȼ����ʱ��T�������������Ƶ�a�㣬�������γ�һ����ֱ���ߣ����㵽a������������ص�b�㣬�Ժ��ظ���һ���̣�����ӵĵ����Ϊe������Ϊm��
������A��B�������ϱ仯�ĵ�ѹ����ÿ������ͨ������ļ���ʱ���ڣ��糡ǿ�ȿ���Ϊ�㶨���䣬��Ҫ��t=0���������ĵ��Ӵ������ϵ�b�㣬Ȼ����ʱ��T�������������Ƶ�a�㣬�������γ�һ����ֱ���ߣ����㵽a������������ص�b�㣬�Ժ��ظ���һ���̣�����ӵĵ����Ϊe������Ϊm��
(1)���AB��������ӵ�ѹ�����ֵ��
(2)д������AB������ѹU��ʱ��t��0��t��T���Ĺ�ϵʽ��
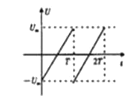
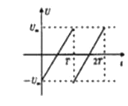
(3)����U��tͼ��
���𰸡�![]() (3)
(3)
����������1������Ӿ�Ua���ٺ���ٶ�Ϊv0�����ݶ��ܶ����ã�eUa��![]() mv02��
mv02��
�����ƫת�ɳ��糡��ˮƽ����ļн�Ϊ���� ![]() ��
��
���Ӵ�ƫת�糡���������U����Ӷ������ƫת�糡������O�������
��ͼ���ɼ��ι�ϵ�ã�
tan����![]() ��
��
�����٢ڢ۽��y=![]() U��
U��
����U=![]() ��
��
��y=s/2ʱ��U�����ֵ��Umax��![]() ��
��
��2��tʱ�̣������λ��![]()
�ɣ�1��ʽ�����У�U(t)��![]() ��
��
��3����ͼ��ʾ��

 ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д� ��������ϵ�д�
��������ϵ�д�