题目内容
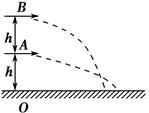
将一篮球从地面上方B点斜向上抛出,刚好垂直击中篮板上A点,不计空气阻力。若抛射点B向篮板方向移动一小段距离,仍使抛出的篮球垂直击中A点,则可行的是( )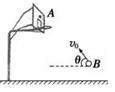
| A.增大抛射速度v0,同时减小抛射角θ |
| B.减小抛射速度v0,同时减小抛射角θ |
| C.增大抛射角θ,同时减小抛出速度v0 |
| D.增大抛射角θ,同时增大抛出速度v0 |
C
解析试题分析:可以将篮球的运动,等效成篮球做平抛运动,当水平速度越大时,抛出后落地速度越大,与水平面的夹角则越小.若水平速度减小,则落地速度变小,但与水平面的夹角变大.因此只有增大抛射角,同时减小抛出速度,才能仍垂直打到篮板上.所以只有C正确,ABD错误,所以本题选择C。
考点: 抛体运动

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
水平抛出的小球,t秒末的速度方向与水平方向的夹角为θ1,t+t0秒末速度方向与水平方向的夹角为θ2,忽略空气阻力,则小球初速度的大小为( )
| A.gt0(cosθ1-cosθ2) | B.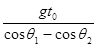 |
| C.gt0(tanθ1-tanθ2) | D.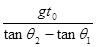 |
如图所示,足够长的斜面上有a、b、c、d、e五个点,ab=bc=cd=de,从a点水平抛出一 个小球,初速度为v时,小球落在斜面上的b点,落在斜面上时的速度方向与斜面夹角 为θ;不计空气阻力,初速度为2v时
| A.小球可能落在斜面上的c点与d点之间 |
| B.小球一定落在斜面上的e点 |
| C.小球落在斜面时的速度方向与斜面夹角大于θ |
| D.小球落在斜面时的速度方向与斜面夹角也为θ |
如图所示,P是水平面上的圆弧凹槽.从高台边B点以速度v0水平飞出的小球,恰能从固定在某位置的凹槽的圆弧轨道的左端A沿圆弧切线方向进入轨道.O是圆弧的圆心,θ1是OA与竖直方向的夹角,θ2是BA与竖直方向的夹角.则( )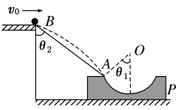
| A.Cotθ1·tanθ2=2 | B.tanθ1·tanθ2=2 |
| C.cotθ1·cotθ2=2 | D.tanθ1·cotθ2=2 |
质点从同一高度水平抛出,不计空气阻力,下列说法正确的是
| A.质量越大,水平位移越大 |
| B.初速度越大,落地时竖直方向速度越大 |
| C.初速度越大,空中运动时间越长 |
| D.初速度越大,落地速度越大 |
物体以速度 水平抛出,若不计空气阻力,则当其竖直分位移与水平位移相等时,以下说法中正确的是( )
水平抛出,若不计空气阻力,则当其竖直分位移与水平位移相等时,以下说法中正确的是( )
| A.竖直分速度等于水平分速度 |
B.瞬时速度大小为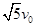 |
C.运动的时间为 |
D.运动的位移为 |
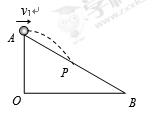
 ,射程为
,射程为 的平抛运动轨迹制成一光滑轨道。一物体由静止开始从轨道顶端滑下,当其到达轨道底部时,物体水平方向速度大小为
的平抛运动轨迹制成一光滑轨道。一物体由静止开始从轨道顶端滑下,当其到达轨道底部时,物体水平方向速度大小为