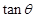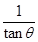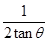题目内容
水平抛出的小球,t秒末的速度方向与水平方向的夹角为θ1,t+t0秒末速度方向与水平方向的夹角为θ2,忽略空气阻力,则小球初速度的大小为( )
| A.gt0(cosθ1-cosθ2) | B.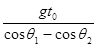 |
| C.gt0(tanθ1-tanθ2) | D.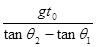 |
D
解析试题分析:如图所示,由平抛运动规律可得:
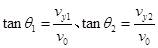 ,同理根据自由落体运动公式可得:
,同理根据自由落体运动公式可得: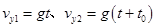 ,联立可得:
,联立可得: ,故小球的初速度的大小
,故小球的初速度的大小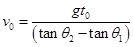 ,所以只有选项D正确;
,所以只有选项D正确;
考点:抛体运动

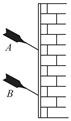
如图,蹲在树枝上的一只松鼠看到一个猎人正在用枪水平瞄准它,就在子弹出枪口时,开始逃跑,松鼠可能的逃跑方式有:①自由落下;②竖直上跳;③迎着枪口,沿AB方向水平跳离树枝;④背着枪口,沿AC方向水平跳离树枝。在这四种逃跑方式中,松鼠不能逃脱厄运而被击中的是(设树枝足够高)( )
| A.①②③ | B.②③④ | C.①③④ | D.①②④ |
如图所示,AB为斜面,BC为水平面,从A点以水平速度v0抛出一小球,此时落点到A点的水平距离为x1,从A点以水平速度3v0抛出小球,这次落点到A点的水平距离为x2,不计空气阻力,则x1∶x2可能等于( )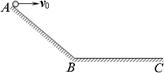
| A.1∶3 | B.1∶6 | C.1∶9 | D.1∶12 |
如图所示,某同学为了找出平抛运动的物体初速度之间的关系,用一个小球在O点对准前方的一块竖直放置的挡板,O与A在同一高度,小球的水平初速度分别是v1、v2、v3,打在挡板上的位置分别是B、C、D,且AB∶BC∶CD=1∶3∶5.则v1、v2、v3之间的正确关系是( )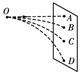
| A.v1∶v2∶v3=6∶3∶2 |
| B.v1∶v2∶v3=5∶3∶1 |
| C.v1∶v2∶v3=3∶2∶1 |
| D.v1∶v2∶v3=9∶4∶1 |
以速度v0水平抛出一小球,忽略空气阻力,当小球的水平速度与竖直速度大小相等时,水平位移与竖直位移的比值是( )
| A.1:1 | B.2:1 | C.1:2 | D.1:4 |
将一篮球从地面上方B点斜向上抛出,刚好垂直击中篮板上A点,不计空气阻力。若抛射点B向篮板方向移动一小段距离,仍使抛出的篮球垂直击中A点,则可行的是( )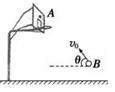
| A.增大抛射速度v0,同时减小抛射角θ |
| B.减小抛射速度v0,同时减小抛射角θ |
| C.增大抛射角θ,同时减小抛出速度v0 |
| D.增大抛射角θ,同时增大抛出速度v0 |
在一次救灾活动中,从水平飞行的直升机上投掷救灾物资。设飞机水平飞行的速度为v0,离地面高度为h,则当物资的速度方向与水平方向成θ时,物资的水平位移x与竖直位移y的关系为(不计空气阻力)
| A.x=ytanθ |
| B.x=2ytanθ |
C.x=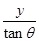 |
D.x=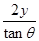 |
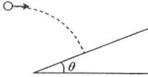
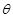 的斜面上时,其速度方向与斜面垂直,运动轨迹如右图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为( )
的斜面上时,其速度方向与斜面垂直,运动轨迹如右图中虚线所示。小球在竖直方向下落的距离与在水平方向通过的距离之比为( )