题目内容
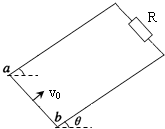 如图所示,质量为m,阻值为R的导体棒ab垂直放在光滑足够长的U形导轨的底端,U形导轨的顶端连接一个阻值为R的电阻,导轨平面与水平面成θ角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,在导体棒上升到最高点的过程中电阻上产生了Q的热量,返回过程中,导体棒在到达底端前已经做匀速运动,速度大小为
如图所示,质量为m,阻值为R的导体棒ab垂直放在光滑足够长的U形导轨的底端,U形导轨的顶端连接一个阻值为R的电阻,导轨平面与水平面成θ角,整个装置处在与导轨平面垂直的匀强磁场中.现给导体棒沿导轨向上的初速度v0,在导体棒上升到最高点的过程中电阻上产生了Q的热量,返回过程中,导体棒在到达底端前已经做匀速运动,速度大小为| v0 | 4 |
(1)导体棒从开始运动到返回底端的过程中,回路中产生的电热;
(2)导体棒上升的最大高度.
(3)导体棒在底端开始运动时的加速度大小.
分析:(1)根据能量的转化与守恒,导体棒减少的动能转化为回路中的电能;
(2)上升的过程中,导体棒的动能转化为它的重力势能和回路的电能.
(3)导体棒在底端开始运动时受到重力、斜面的支持力和安培力的作用,沿斜面的方向重力的分力与安培力提供加速度,根据牛顿第二定律即可求出加速度;
(2)上升的过程中,导体棒的动能转化为它的重力势能和回路的电能.
(3)导体棒在底端开始运动时受到重力、斜面的支持力和安培力的作用,沿斜面的方向重力的分力与安培力提供加速度,根据牛顿第二定律即可求出加速度;
解答:解:(1)根据能量守恒定律,得:
Q总=
mv02-
m(
)2=
…①
(2)设上升的最大高度为h,由动能定理有:
-mgh+WF安=0-
mv02…②
电阻R上产生的热量为Q,导体棒与电阻的阻值相等,则整个回路上升过程中产生的热量为2Q,
WF安=-2Q…③
h=
…④
(3)在底端,设棒上电流为I,加速度为a,由牛顿第二定律,则:mgsinθ+BIL=ma…⑤
由欧姆定律,得:I=
…⑥
E=BLv0…⑦
棒到达底端前已经做匀速运动mgsinθ=
…⑧
以上方程联立可得:a=5gsinθ…⑨
答:(1)回路中产生的电热
(2)导体棒上升的最大高度
(3)导体棒在底端开始运动时的加速度大小5gsinθ.
Q总=
| 1 |
| 2 |
| 1 |
| 2 |
| v0 |
| 4 |
| 15mv02 |
| 32 |
(2)设上升的最大高度为h,由动能定理有:
-mgh+WF安=0-
| 1 |
| 2 |
电阻R上产生的热量为Q,导体棒与电阻的阻值相等,则整个回路上升过程中产生的热量为2Q,
WF安=-2Q…③
h=
| mv02-4Q |
| 2mg |
(3)在底端,设棒上电流为I,加速度为a,由牛顿第二定律,则:mgsinθ+BIL=ma…⑤
由欧姆定律,得:I=
| E |
| 2R |
E=BLv0…⑦
棒到达底端前已经做匀速运动mgsinθ=
B2L2
| ||
| 2R |
以上方程联立可得:a=5gsinθ…⑨
答:(1)回路中产生的电热
1
| ||
| 32 |
(2)导体棒上升的最大高度
| ||
| 2mg |
(3)导体棒在底端开始运动时的加速度大小5gsinθ.
点评:解决这类问题的关键时分析受力,进一步确定运动性质,并明确判断各个阶段及全过程的能量转化.在计算导体棒上升的最大高度时用到积分的概念

练习册系列答案
相关题目
 如图所示,质量为m的球,被长为L的细绳吊起处于静止状态.现对小球施加水平向右的恒力F,小球开始向右运动,当细绳与竖直方向的夹角为60°,小球速度恰好为0( )
如图所示,质量为m的球,被长为L的细绳吊起处于静止状态.现对小球施加水平向右的恒力F,小球开始向右运动,当细绳与竖直方向的夹角为60°,小球速度恰好为0( )

 (2010?黑龙江模拟)(按题目要求作答,写出必要的文字说明、方程式和重要演算步骤,只写出最后答案不得分)
(2010?黑龙江模拟)(按题目要求作答,写出必要的文字说明、方程式和重要演算步骤,只写出最后答案不得分) (2005?青浦区模拟)如图所示,质量为m的带电金属小球,用绝缘细线与质量为M(M=2m)的不带电木球相连,两球恰能在竖直向上的足够大且场强为E的匀强电场中,以速度v匀速竖直向上运动,当木球升至a点时,细线突然断裂,木球升至b点时速度为零.则木球速度为零时,金属球的速度大小为
(2005?青浦区模拟)如图所示,质量为m的带电金属小球,用绝缘细线与质量为M(M=2m)的不带电木球相连,两球恰能在竖直向上的足够大且场强为E的匀强电场中,以速度v匀速竖直向上运动,当木球升至a点时,细线突然断裂,木球升至b点时速度为零.则木球速度为零时,金属球的速度大小为 (2003?徐州一模)如图所示,质量为M的木板可以沿倾角为α的固定斜面无摩擦地滑下,欲使木板静止在斜面上,木板上质量为m的人应以多大的加速度向下奔跑?
(2003?徐州一模)如图所示,质量为M的木板可以沿倾角为α的固定斜面无摩擦地滑下,欲使木板静止在斜面上,木板上质量为m的人应以多大的加速度向下奔跑?