题目内容
19.已知金刚石的密度是3500kg/m3,摩尔质量为1.2×10-2kg/mol,有一小块金刚石,体积是4.0×10-8m3,这小块金刚石中含有多少个碳原子?设想金刚石中碳原子是紧密地堆在一起的,估算碳原子的直径.分析 根据摩尔数=$\frac{质量}{摩尔质量}$;分子数=摩尔数×阿伏加德罗常数,求碳原子数目.
设想金刚石中碳原子是紧密地堆在一起的,碳原子的体积等于体积除以碳原子的数目,从而可求出碳原子的直径.
解答 解:金刚石的质量:m=ρV=3500×4.0×10-8kg=1.4×10-4 kg
摩尔数为:n=$\frac{m}{M}$=$\frac{1.4×1{0}^{-4}}{1.2×1{0}^{-2}}$=1.17×10-2mol
碳原子数为:N=nNA=1.17×10-2×6.02×1023≈7.0×1021个
一个碳原子的体积为:V0=$\frac{V}{N}$=$\frac{4×1{0}^{-8}}{7×1{0}^{21}}$≈5.7×10-30 m3
把金刚石中的碳原子看成球体,则由公式V0=$\frac{π}{6}{d}^{3}$
可得碳原子直径为:d=$\root{3}{\frac{6{V}_{0}}{π}}$=$\root{3}{\frac{6×5.7×1{0}^{-30}}{3.14}}$≈2.2×10-10m
答:这小块金刚石中含有7.0×1021个碳原子.设想金刚石中碳原子是紧密地堆在一起的,碳原子的直径约为2.2×10-10m.
点评 本题是阿伏加德罗常数的运用问题,要明确其是联系宏观与微观的桥梁.要建立清晰的碳原子模型,将碳原子看成球形或立方体形,再求解其直径.

练习册系列答案
相关题目
9. 倾角θ=30°的斜面AB粗糙且绝缘,C为AB上的一点,且BC长为1m,在AC间放有一根平行于斜面的绝缘轻质弹簧,在弹簧所在区域内加一方向垂直斜面向上的匀强磁场,C为电场的边界线,电场强度E=$\frac{\sqrt{3}mg}{2q}$,如图所示.现有一质量为m、电荷量为q可视为质点带正电的小物块,从B点开始以速度2m/s沿斜面向下匀速运动,接触弹簧后做变速运动,最后又被弹出电场区域,若弹簧始终在弹性限度内,重力加速度g=10m/s2,则下列有关描述中正确的有( )
倾角θ=30°的斜面AB粗糙且绝缘,C为AB上的一点,且BC长为1m,在AC间放有一根平行于斜面的绝缘轻质弹簧,在弹簧所在区域内加一方向垂直斜面向上的匀强磁场,C为电场的边界线,电场强度E=$\frac{\sqrt{3}mg}{2q}$,如图所示.现有一质量为m、电荷量为q可视为质点带正电的小物块,从B点开始以速度2m/s沿斜面向下匀速运动,接触弹簧后做变速运动,最后又被弹出电场区域,若弹簧始终在弹性限度内,重力加速度g=10m/s2,则下列有关描述中正确的有( )
 倾角θ=30°的斜面AB粗糙且绝缘,C为AB上的一点,且BC长为1m,在AC间放有一根平行于斜面的绝缘轻质弹簧,在弹簧所在区域内加一方向垂直斜面向上的匀强磁场,C为电场的边界线,电场强度E=$\frac{\sqrt{3}mg}{2q}$,如图所示.现有一质量为m、电荷量为q可视为质点带正电的小物块,从B点开始以速度2m/s沿斜面向下匀速运动,接触弹簧后做变速运动,最后又被弹出电场区域,若弹簧始终在弹性限度内,重力加速度g=10m/s2,则下列有关描述中正确的有( )
倾角θ=30°的斜面AB粗糙且绝缘,C为AB上的一点,且BC长为1m,在AC间放有一根平行于斜面的绝缘轻质弹簧,在弹簧所在区域内加一方向垂直斜面向上的匀强磁场,C为电场的边界线,电场强度E=$\frac{\sqrt{3}mg}{2q}$,如图所示.现有一质量为m、电荷量为q可视为质点带正电的小物块,从B点开始以速度2m/s沿斜面向下匀速运动,接触弹簧后做变速运动,最后又被弹出电场区域,若弹簧始终在弹性限度内,重力加速度g=10m/s2,则下列有关描述中正确的有( )| A. | 粗糙斜面的动摩擦因数为$\frac{\sqrt{3}}{3}$ | |
| B. | 小物块进入电场向下压缩弹簧的过程中先加速后减速运动 | |
| C. | 小物块进入电场后小物块和弹簧组成的系统机械能减小 | |
| D. | 小物块最后停在BC间,距C点0.3m处 |
14.下列关于速度和加速度的说法中正确的是( )
| A. | 物体加速度增大,速度就增大 | |
| B. | 物体速度变化得越快,速度就越大 | |
| C. | 物体速度越大,速度的变化率就越大 | |
| D. | 物体运动快慢和运动速度变化快慢不是一样的 |
1.以速度v0水平抛出一小球,不计空气阻力,从抛出时刻开始计时,经t1时间小球到达竖直分速度与水平分速度大小相等的A点,经t2时间小球到达竖直分位移与水平分位移大小相等的B点,下列判断正确的是( )
| A. | t1、t2的大小与v0的大小有关 | B. | t2=2t1 | ||
| C. | A、B两点速度大小之比为$\sqrt{2}$:$\sqrt{5}$ | D. | A、B两点的高度差为$\frac{3{{v}_{0}}^{2}}{2g}$ |
2.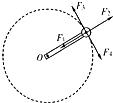 如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
 如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )
如图所示,一根质量不计的轻杆绕水平固定转轴O顺时针匀速转动,另一端固定有一个质量m的小球,当小球运动到图中位置时,轻杆对小球作用力的方向可能( )| A. | 沿F2的方向 | B. | 沿F1的方向 | C. | 沿F3的方向 | D. | 沿F4的方向 |
 在“探究气体等温变化的规律”实验中,封闭的空气如图甲所示,U型玻璃管粗细均匀,右端开口,己知外界大气压为76cm汞柱高,通过向U型玻璃管开口端缓慢注入水银可以改变气体的状态.
在“探究气体等温变化的规律”实验中,封闭的空气如图甲所示,U型玻璃管粗细均匀,右端开口,己知外界大气压为76cm汞柱高,通过向U型玻璃管开口端缓慢注入水银可以改变气体的状态.
 某同学用如图所示的实验器材探究电磁感应现象.他连接好电路并检查无误后,闭合电键的瞬间观察到电流表G指针向右偏转,电键闭合后,他还进行了下列操作:将滑动变阻器的滑动触头P快速向接线柱C移动,电流计指针将右偏(填“左偏”、“右偏”或“不偏”).
某同学用如图所示的实验器材探究电磁感应现象.他连接好电路并检查无误后,闭合电键的瞬间观察到电流表G指针向右偏转,电键闭合后,他还进行了下列操作:将滑动变阻器的滑动触头P快速向接线柱C移动,电流计指针将右偏(填“左偏”、“右偏”或“不偏”). 如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以5.0m/s的初速度向平台边缘匀速滑去,(取重力加速度g=10m/s2).求:
如图所示,高为h=1.25m的平台上,覆盖一层薄冰,现有一质量为60kg的滑雪爱好者,以5.0m/s的初速度向平台边缘匀速滑去,(取重力加速度g=10m/s2).求: