题目内容
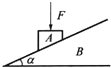
【题目】如图甲所示,质量为M=4 kg的木板静止在水平面上,质量m=1 kg的小滑块静止在木板的右端,可看成质点,已知木板与水平面间的动摩擦因数μ1=0.1,小滑块与木板间的动摩擦因数μ2=0.4,重力加速度g=10 m/s2。现用力F作用在木板M上,F随时间t变化的关系如图乙所示,求:
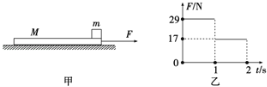
(1)t=1 s时,小滑块和木板的速度大小;
(2)为使小滑块不从木板上滑落下来,木板的最小长度。
【答案】(1)vm =4 m/s,vM =5 m/s (2)木板的最小长度L=0.75 m
【解析】(1)小滑块受到的摩擦力提供加速度,设小滑块的加速度是a1,则有:
a1=![]() =μ2g=0.4×10 m/s2=4 m/s2
=μ2g=0.4×10 m/s2=4 m/s2
对木板,设第1 s内木板的加速度为a2,则有:
a2=![]() m/s2=5 m/s2
m/s2=5 m/s2
设木板在第2s内的加速度为a3,则有:
a3=![]() m/s2=2 m/s2
m/s2=2 m/s2
t=1 s时,小滑块的速度为:vm=a1t=4×1 m/s=4 m/s
木板的速度为:vM=a2t=5×1 m/s=5 m/s
(2)由于a3<a1,当滑块与木板速度相等时,滑块与木板将保持相对静止,一起运动,得:a1t+a1Δt=a2t+a3Δt
解得:Δt=0.5 s
滑块与木板在1.5s时保持相对静止,0~1.5 s内,木板的位移:
s2=![]() a2 t2+ a2tΔt+
a2 t2+ a2tΔt+![]() a3Δt2=
a3Δt2=![]() ×5×12 m +5×1×0.5 m +
×5×12 m +5×1×0.5 m +![]() ×2×0.52 m =5.25 m
×2×0.52 m =5.25 m
滑块的位移为:
s1=![]() a1 t2+ a1tΔt+
a1 t2+ a1tΔt+![]() a1Δt2=
a1Δt2=![]() ×4×12 m +4×1×0.5 m +
×4×12 m +4×1×0.5 m +![]() ×4×0.52 m =4.5 m
×4×0.52 m =4.5 m
木板的最小长度:L=s2-s1=5.25 m-4.5 m=0.75 m

练习册系列答案
相关题目