题目内容
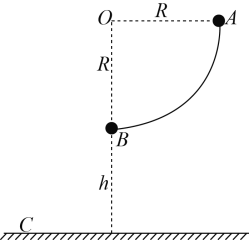
【题目】在一化肥厂有如图所示的传送装置,AB 为水平,长 l1 =4m,顺时针传动的速率 v1 = 5m / s,CD 为靠近 AB 的倾斜传送带,q = 37 ,长 l2 =5.3m,两表面 动摩擦因数 μ=0.5,一袋标准化肥的质量 m=20kg. 已知 sin 37 =0.6、 cos 37 =0.8、 g=10m/s2
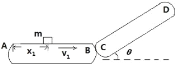
(1)CD 传送带不动时,问一袋化肥从离 A 端 x1 的位置处轻放在去,则在 CD 上上升的最大距离为 x2,求 x2 与 x1 的关系?
(2)若化肥从 A 端轻放上去,并使 CD 顺时针以速率 v 传动,问 v 应满足什么条 件才能使化肥送至顶点 D?
【答案】(1) x2=1.25m(0≤x1≤1.5m)或x2=20.5x1(1.5m≤x1≤4m);(2) v ![]() 4.5m/s
4.5m/s
【解析】
(1)物体在水平传送带摩擦力的作用下,先向右加速,根据牛顿第二定律可求得加速度,根据位移公式可求加速运动的位移,在离A端距离x0≤x1处放上时,能在CD传送带上上升的距离相同.上升时为加速度为a2的匀减速运动;
(2)分析物体滑上倾斜传送带的运动,以加速度a′=gsinθ-μgcosθ减速运动减速到与带同速,后又减速到零,结合运动学公式可求.
(1)设从离A端x0轻放上化肥时,刚好能在B端与传送带达到同等速度,化肥放上后的加速度为a1.则:
μmg=ma1 ①
x0=L1![]() ②
②
解得:a1=5m/s2,x0=1.5m
在离A端距离x0≤x1处放上时,能在CD传送带上上升的距离相同.上升时为加速度为a2的匀减速运动:mgsinθ+μmgcosθ=ma2 ③
v12=2a2x2 ④
解得:a2=10m/s2、x2=1.25m
当x0≤x1≤L1时,在拐点处的速度为vx
vx2=2a2x2=2a1(L-x1) ⑤
解得:x2=2-0.5x1
综上所述x2=1.25m(0≤x1≤1.5m)或x2=20.5x1(1.5m≤x1≤4m)
(2)从A端放上去,设CD传动速度为v2时,化肥恰好能到达D端;假设v2<v1,则化肥经历了两个减速阶段,第一阶段从C点到减速至v2,加速度为a2;达到v2后以a3继续减速至0,则:
mgsinθ-μmgcosθ=ma3 ⑦![]() ⑧
⑧
联立⑦⑧可得v2=4.5m/s并验证了假设成立,所以条件为v≥4.5m/s