题目内容
【题目】在t=0的时刻,从地面附近的空中某点释放一小球,它自由下落,落地后反弹,且每次反弹都能到达最初的出发点,取竖直向上为正方向.设小球与地面的碰撞时间和小球在空中所受空气阻力都忽略不计,则小球的速度v随时间t变化的关系可表示为图中的哪个( )
A. 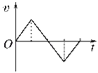 B.
B. 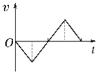 C.
C. 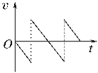 D.
D. 
【答案】C
【解析】试题分析:小球做自由落体运动,落地前做匀加速直线运动,与地面发生碰撞反弹速度与落地速度大小相等,方向相反,然后向上做匀减速直线运动,根据速度时间关系即可求解.
解:A、小球自由落下,若从释放时开始计时,速度v=gt,方向向下,与规定的正方向相反,所以速度是负值,与地面发生碰撞反弹速度与落地速度大小相等,方向相反即向上,速度为正,向上做匀加速直线运动直到速度为0,然后重复上面的过程.
故C正确.

练习册系列答案
相关题目








