Question

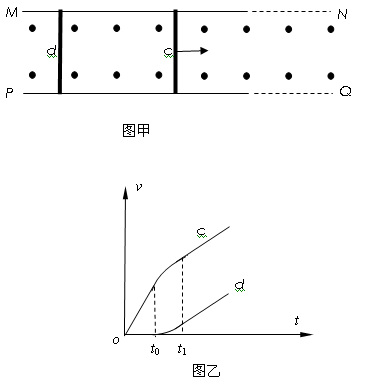
（16分）如图甲所示，相距为L的两平行金属导轨MN、PQ固定在绝缘水平面上，处于竖直向上的匀强磁场中，磁场的磁感应强度为B，导轨足够长且电阻不计．两相同金属棒c和d与导轨垂直放置，它们的质量均为m，电阻均为R，间距为s₀，与导轨间动摩擦因数均为μ，设最大静摩擦力与滑动摩擦力相等．在t=0时刻，对c棒施加一水平向右的力，使其从静止开始做匀加速直线运动．在t₀时刻，d棒开始运动，此后保持水平力不变，由速度传感器测得两金属棒的v―t图象如图乙所示，从t₁时刻开始两金属棒以相同的加速度做匀加速直线运动，此时两金属棒的间距为s．试求：

（1）在0至t₁时间内通过c棒的电量；

（2）t₀时刻回路的电功率和c棒的速度大小；

（3）t₁时刻开始两金属棒的加速度大小。

Answer 1

解析：

 

（1）从0至t₁这段时间内              （1分）

又                                  （2分）

解得                                       （1分）

（2）设在t₀时刻回路的瞬时感应电流为I，则对d棒

由平衡条件得                          （1分）

t₀时刻回路的电功率                             （1分）

 解得                                      （1分）

对回路由全电路欧姆定律有                        （2分）

解得                                         （1分）

（3）设在t₀时刻，水平外力为F₀，棒c的加速度为a₀，由牛顿第二定律得

                                     （2分）

而                                                （1分）

从t₁时刻起，对两金属棒组成的系统，由牛顿第二定律有

                                                      （1分）

解得                                                    （2分）