题目内容
(2009?南通一模)如图甲所示,相距为L的两平行金属导轨MN、PQ固定在绝缘水平面上,处于竖直向上的匀强磁场中,磁场的磁感应强度为B,导轨足够长且电阻不计.两相同金属棒c和d与导轨垂直放置,它们的质量均为m,电阻均为R,间距为s0,与导轨间动摩擦因数均为μ,设最大静摩擦力与滑动摩擦力相等.在t=0时刻,对c棒施加一水平向右的力,使其从静止开始做匀加速直线运动.在t0时刻,d棒开始运动,此后保持水平力不变,由速度传感器测得两金属棒的v-t图象如图乙所示,从t1时刻开始两金属棒以相同的加速度做匀加速直线运动,此时两金属棒的间距为s.试求:
(1)在0至t1时间内通过c棒的电量;
(2)t0时刻回路的电功率和c棒的速度大小;
(3)t1时刻开始两金属棒的加速度大小.

(1)在0至t1时间内通过c棒的电量;
(2)t0时刻回路的电功率和c棒的速度大小;
(3)t1时刻开始两金属棒的加速度大小.

分析:(1)根据法拉第电磁感应定律求出平均电流,带入公式Q=It即可求出电量.
(2)根据题意:在t0时刻,d棒开始运动,d棒受力平衡可求解感应电流,根据功率公式和E=BLV即可求解;
(3)在0至t0这段时间内C棒做匀加速直线运动,根据v=at可求C棒在t0时刻的加速度,又此后保持水平力不变,对C棒有牛顿第二定律可求外力,然后对Cd整体由牛顿第二定律列式求解即可求出共同加速度.
(2)根据题意:在t0时刻,d棒开始运动,d棒受力平衡可求解感应电流,根据功率公式和E=BLV即可求解;
(3)在0至t0这段时间内C棒做匀加速直线运动,根据v=at可求C棒在t0时刻的加速度,又此后保持水平力不变,对C棒有牛顿第二定律可求外力,然后对Cd整体由牛顿第二定律列式求解即可求出共同加速度.
解答:解:(1)根据法拉第电磁感应定律得从0至t1这段时间内产生平均感应电动势为:
E=
=
…①
由闭合电路欧姆定律得感应电流为:I=
… ②
在0至t1时间内通过c棒的电量为:q=It1… ③
①②③联立得:q=
(2)设在t0时刻回路的瞬时感应电流为I,则对d棒,由平衡条件得
BIL=μmg…④
t0时刻回路的电功率为:P=I2×2R…⑤
④⑤联立解得:P=
对回路由闭合电路欧姆定律有:I=
…⑥
④⑥联立解得:vc=
…⑦
(3)设在t0时刻,水平外力为F0,棒c的加速度为a0,
根据v=at得C棒在t0时刻的加速度为:a0=
…⑧
对C棒由牛顿第二定律得:F0-μmg-BIL=ma0…⑨
从t1时刻起,对两金属棒组成的系统,由牛顿第二定律得:F0-2μmg=2ma…⑩
⑦⑧⑨⑩联立解得:a=
答:(1)在0至t1时间内通过c棒的电量q=
;
(2)t0时刻回路的电功率和c棒的速度大小vc=
;
(3)t1时刻开始两金属棒的加速度大小a=
.
E=
| N△? |
| △t |
| BL(S-S0)□ |
| t1 |
由闭合电路欧姆定律得感应电流为:I=
| E |
| 2R |
在0至t1时间内通过c棒的电量为:q=It1… ③
①②③联立得:q=
| BL(S-S0) |
| 2R |
(2)设在t0时刻回路的瞬时感应电流为I,则对d棒,由平衡条件得
BIL=μmg…④
t0时刻回路的电功率为:P=I2×2R…⑤
④⑤联立解得:P=
| 2μ2m2g2R |
| B2L2 |
对回路由闭合电路欧姆定律有:I=
| BLV |
| 2R |
④⑥联立解得:vc=
| 2μmgR |
| B2L2 |
(3)设在t0时刻,水平外力为F0,棒c的加速度为a0,
根据v=at得C棒在t0时刻的加速度为:a0=
| vc |
| t0 |
对C棒由牛顿第二定律得:F0-μmg-BIL=ma0…⑨
从t1时刻起,对两金属棒组成的系统,由牛顿第二定律得:F0-2μmg=2ma…⑩
⑦⑧⑨⑩联立解得:a=
| μmgR |
| B2L2t0 |
答:(1)在0至t1时间内通过c棒的电量q=
| BL(S-S0) |
| 2R |
(2)t0时刻回路的电功率和c棒的速度大小vc=
| 2μmgR |
| B2L2 |
(3)t1时刻开始两金属棒的加速度大小a=
| μmgR |
| B2L2t0 |
点评:电磁感应中导体切割引起的感应电动势在考试中涉及较多,应明确导体棒受力分析、功能关系等的灵活应用,注意平衡状态的处理.解决本题的关键会根据牛顿第二定律求加速度.

练习册系列答案
相关题目
 (2009?南通一模)如图所示,水平放置的平行板电容器与一直流电源相连,在两板中央有一带电液滴处于静止状态.现通过瞬间平移和缓慢平移两种方法将A板移到图中虚线位置.下列关于带电液滴运动的说法中正确的是( )
(2009?南通一模)如图所示,水平放置的平行板电容器与一直流电源相连,在两板中央有一带电液滴处于静止状态.现通过瞬间平移和缓慢平移两种方法将A板移到图中虚线位置.下列关于带电液滴运动的说法中正确的是( )
 (2009?南通一模)如图是磁流体发电机的示意图,在间距为d的平行金属板A、C间,存在磁感应强度为B、方向垂直纸面向外的匀强磁场,两金属板通过导线与变阻器R相连,等离子体以速度v平行于两金属板垂直射入磁场.若要增大该发电机的电动势,可采取的方法是等离子体RAC( )
(2009?南通一模)如图是磁流体发电机的示意图,在间距为d的平行金属板A、C间,存在磁感应强度为B、方向垂直纸面向外的匀强磁场,两金属板通过导线与变阻器R相连,等离子体以速度v平行于两金属板垂直射入磁场.若要增大该发电机的电动势,可采取的方法是等离子体RAC( )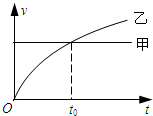 (2009?南通一模)甲、乙两物体从同一地点沿同方向做直线运动,运动的v-t图象如图所示,下列说法中正确的是( )
(2009?南通一模)甲、乙两物体从同一地点沿同方向做直线运动,运动的v-t图象如图所示,下列说法中正确的是( )