题目内容
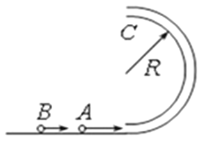
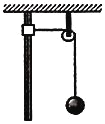
【题目】如图所示，轻质绝缘细线的上端固定在天花板上，下端拴着一个质量为m的带电小球，细线长为L，当空间中加上一个水平向右的匀强电场时，小球由静止开始从A点向左边摆动，经过B点之后到达最高点C。小球经过B点时，细线与竖直方向夹角为37°角，到达C点时，细线与竖直方向成74°角，sin37°=0.6,cos37°=0.8,当地重力加速度为g，求：
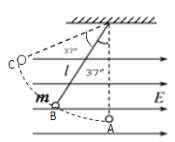
(1)小球经过B点时，细线的拉力是多少？
(2)若保持电场强度的大小不变，将其方向变为竖直向下，让小球从B点由静止释放，小球经过A点时，细线的拉力是多少？
【答案】(1)
(2)
【解析】
(1)将小球受到的电场力和重力的合力看成等效重力，由几何关系可知，A、C两点关于B点对称，所以B点是等效最低点，此时细线与等效重力共线。由平行四边形定则得
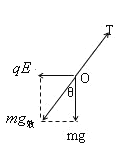
小球从A点运动到B点时，由动能定理得
小球处在B点时，由牛顿第二定律得
联立以上各式得
(2)当电场强度的方向变成竖直向下以后，小球受到的电场力方向为竖直向上，小球从B点运动到A点时，由动能定理得
小球处在A点时，由牛顿第二定律得
联立各式解得
答：(1)(2)
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
