题目内容
5. 如图所示,一质量m=2×10-11kg,q=1.0×10-5 C的带电粒子(重力不计),初速度为零经U1=100V的加速电压加速后,水平进入极板长L=20cm,极板间距d=10$\sqrt{3}$cm的偏转电场中
如图所示,一质量m=2×10-11kg,q=1.0×10-5 C的带电粒子(重力不计),初速度为零经U1=100V的加速电压加速后,水平进入极板长L=20cm,极板间距d=10$\sqrt{3}$cm的偏转电场中(1)粒子进入偏转电场时速度多大?
(2)若使粒子射出偏转电场时,以与水平方向成θ=30°角的方向进入一个匀强磁场区域,则偏转电压为多大?
(3)若水平匀强磁场的宽度D=30cm,使带电粒子不能由磁场右边射出,磁感应强度B至少多大?
分析 粒子在加速电场中,电场力做功,由动能定理求出速度v.粒子进入偏转电场后,做类平抛运动,运用运动的合成与分解,由牛顿第二定律和运动学公式求出电压U2.
粒子进入磁场后做匀速圆周运动,结合条件,画出临界情况的运动轨迹,由几何知识求半径的最大值,再由洛伦兹力提供向心力求出B的最小值.
解答 解: (1)带电微粒在加速电场加速运动的过程,根据动能定理得:
(1)带电微粒在加速电场加速运动的过程,根据动能定理得:
qU1=$\frac{1}{2}m{{v}_{0}}^{2}$
则得:v0=$\sqrt{\frac{2q{U}_{1}}{m}}=\sqrt{\frac{2×1×1{0}^{5}×100}{2×1{0}^{-11}}}$m/s=1.0×104m/s,
(2)带电微粒在偏转电场中只受电场力作用,做类平抛运动.在水平方向微粒做匀速直线运动
水平方向有:L=v0t
带电微粒在竖直方向做匀加速直线运动,加速度为a,
出电场时竖直方向速度为vy,
竖直方向:vy=at,a=$\frac{q{U}_{2}}{md}$,得:vy=$\frac{q{U}_{2}}{md}•\frac{L}{v}$.
由速度分解关系得:tanθ=$\frac{{v}_{y}}{{v}_{0}}$
联立以上两式解得:U2=100V,
(3)带电微粒进入磁场做匀速圆周运动,洛伦兹力提供向心力,设微粒轨迹恰好与磁场右边相切时半径为R.
由几何关系知
R+Rsin30°=D
设微粒进入磁场时的速度为v′,则 v′=$\frac{{v}_{0}}{cos30°}$
由牛顿运动定律及运动学规律得:qv′B=m$\frac{v{′}^{2}}{R}$
解得:B=$\frac{\sqrt{3}}{15}$T
所以带电粒子不射出磁场右边,磁感应强度B至少为$\frac{\sqrt{3}}{15}$T.
答:(1)粒子进入偏转电场时速度为1×104m/s;
(2)若使粒子射出偏转电场时,以与水平方向成θ=30°角的方向进入一个匀强磁场区域,则偏转电压为100V;
(3)若水平匀强磁场的宽度D=30cm,使带电粒子不能由磁场右边射出,磁感应强度B至少为$\frac{\sqrt{3}}{15}$T.
点评 本题是带电粒子在组合场中运动的问题,关键是分析粒子的受力情况和运动情况,用力学的方法处理,在磁场中做匀速圆周运动时,能画出粒子运动的轨迹,并根据几何关系求出半径,难度适中.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | 鸡蛋碰石头,虽然鸡蛋碎了而石头完好无损,但鸡蛋对石头的作用力和石头对鸡蛋的作用力是完全相同的 | |
| B. | 只有能运动的物体才会施力,静止的物体只能受到力而不会施力 | |
| C. | “风吹草低见牛羊”,草受到了力而弯曲,但未见到施力物体,说明没有施力物体的力也是可以存在的 | |
| D. | 任何一个物体,一定既是受力物体,也是施力物体 |
| A. | 当氢原子从n=2的状态跃迁到n=6的状态时,发射出光子 | |
| B. | 如果紫光能使某种金属产生光电效应,则X射线一定能让该金属发生光电效应 | |
| C. | β射线粒子和阴极射线实质都是电子,而γ射线则是电磁波 | |
| D. | 铀核裂变时放出能量,中子与质子结合成氘核时也放出能量 |
| A. | 飞船的轨道半径 | B. | 飞船的质量 | C. | 飞船的运行周期 | D. | 行星的质量 |
 图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,其传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近.水平部分AB以v0=5m/s的速率顺时针转动.将一袋质量为10kg的大米无初速度放在A端,到达B端后,米袋继续沿倾斜的CD部分运动,不计米袋在BC处的机械能损失.已知米袋与传送带间的动摩擦因数均为0.5,g=10m/s2,cos 37°=0.8,求:
图示为仓库中常用的皮带传输装置示意图,它由两台皮带传送机组成,一台水平传送,A、B两端相距3m,另一台倾斜,其传送带与地面的倾角θ=37°,C、D两端相距4.45m,B、C相距很近.水平部分AB以v0=5m/s的速率顺时针转动.将一袋质量为10kg的大米无初速度放在A端,到达B端后,米袋继续沿倾斜的CD部分运动,不计米袋在BC处的机械能损失.已知米袋与传送带间的动摩擦因数均为0.5,g=10m/s2,cos 37°=0.8,求:

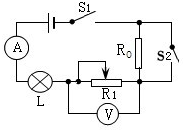 如图所示的电路中,小灯泡L上标有“6V 6W”字样(忽略温度对灯丝电阻的影响,电表为理想电表)
如图所示的电路中,小灯泡L上标有“6V 6W”字样(忽略温度对灯丝电阻的影响,电表为理想电表)