题目内容
【题目】如图所示,足够大的平行挡板A1、A2竖直放置,间距6L.两板间存在两个方向相反的匀强磁场区域Ⅰ和Ⅱ,以水平面MN为理想分界面,Ⅰ区的磁感应强度为B0,方向垂直纸面向外.A1、A2上各有位置正对的小孔S1、S2,两孔与分界面MN的距离均为L.质量为m、电量为+q的粒子经宽度为d的匀强电场由静止加速后,沿水平方向从S1进入Ⅰ区,并直接偏转到MN上的P点,再进入Ⅱ区,P点与A1板的距离是L的k倍,不计重力,碰到挡板的粒子不予考虑.
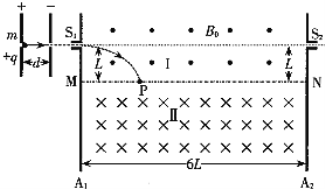
(1)若k=1,求匀强电场的电场强度E;
(2)若2<k<3,且粒子沿水平方向从S2射出,求出粒子在磁场中的速度大小v与k的关系式和Ⅱ区的磁感应强度B与k的关系式.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)粒子在电场中,由动能定理有qEd=![]() mv2-0 ①
mv2-0 ①
粒子在Ⅰ区洛伦兹力提供向心力 qvB0=![]() ②
②
当k=1时,由几何关系得 r=L ③
由①②③解得E=![]() ④
④
(2)由于2<k<3时,由题意可知粒子在Ⅱ区只能发生一次偏转,由几何关系可知
(r-L)2+(kL)2=r2⑤
解得r=![]() ⑥
⑥
由②⑥解得v=![]() ⑦
⑦
粒子在Ⅱ区洛伦兹力提供向心力 qvB=![]() ⑧
⑧
由对称性及几何关系可知![]() ⑨
⑨
解得r1=![]() ⑩
⑩
由⑧⑩解得 B=![]()

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目