题目内容
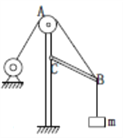
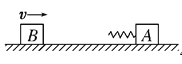
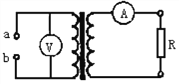
【题目】如图是工厂流水生产线包装线示意图,质量均为m=2.5kg、长度均为l=0.36m的产品在光滑水平工作台AB上紧靠在一起排列成直线(不粘连),以v0=0.6m/s的速度向水平传送带运动,设当每个产品有一半长度滑上传送带时,该产品即刻受到恒定摩擦力Ff=μmg而做匀加速运动,当产品与传送带间没有相对滑动时,相邻产品首尾间距离保持2l(如图)被依次送入自动包装机C进行包装。观察到前一个产品速度达到传送带速度时,下一个产品刚好有一半滑上传送带而开始做匀加速运动。取g=10m/s2。试求:

(1)传送带的运行速度v;
(2)产品与传送带间的动摩擦因数μ:
(3)满载工作时与空载时相比,传送带驱动电动机增加的功率P;
(4)为提高工作效率,工作人员把传送带速度调成v'=2.4m/s,已知产品送入自动包装机前已匀速运动,求第(3)问中的P′?第(3)问中在相当长时间内的等效P′′?
【答案】(1)1.8m/s (2) μ=0.2 (3)9W (4)18W
【解析】(1)产品在平台和传送带上不积压、不断流,则产品在平台上运动l与在传送带上最终
运动3l距离所用时间相等设为t,则t=![]()
解得他送带速度v=3v0=1.8m/s,t=0.6s
(2)解法一:产品滑上传送带后做初速度为v0的匀加速运动,设加速时间为t′,依题意,
前一个产品加速结束时下一个产品刚好开始加速,因此t′=t=0.6s
由速度公式得v=v0+a t′
由牛顿第二定律Ff=ma
联立代入Ff=μmg
解得μ=0.2
解法二:产品滑上传送带后做初速度为v0的匀加速运动,设加速时间为t',则从前一个产品加速开始,到下一个产品达到传送带速皮所用时间为2t'。
对前一个产品![]()
对下一个产品![]()
且x1-x2=3l
解得t'=0.6s
由速度公式得v=v0+at'
由牛顿第二定律可知Ff=ma
联立代入Ff=μmg
解得μ=0.2
(3)由t'=0.6s=t可知,传送带上始终只有一个产品正在加速,
所以传送带驱动电动机增加的功率P=Ffv
联立解得P=9W
(4)两种情况,若是两个产品正在加速P=Ffv=24W,若是一个产品正在加速P=Ffv=12W
时间足够长,两个产品加速和一个产品加速的时间近似相等,等效的P=(24+12)/2=18W