题目内容
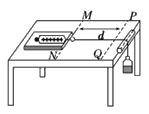
【题目】一个质量m=0.1g的小滑块,带有q=5×10-4C的电荷放置在倾角θ=30°的光滑斜面上(绝缘),斜面置于B=0.5T的匀强磁场中,磁场方向垂直纸面向里,如图所示,小滑块由静止开始沿斜面滑下,其斜面足够长,小滑块滑至某一位置时,要离开斜面。求:

①小滑块带何种电荷?
②小滑块离开斜面的瞬时速度多大?
③该斜面的长度至少多长?
【答案】①小滑块带负电荷 ②v=3.4m/s ③s=1.2m
【解析】试题分析:(1)小滑块沿斜面下滑过程中,受重力mg、斜面支持力FN和洛伦兹力F。若要小滑块离开斜面,洛伦兹力F方向应垂直斜面向上,根据左手定则可知,小滑块应带有负电荷。
(2)小滑块沿斜面下滑时,垂直斜面方向的合外力为零,有qvB+FN-mgcosα=0
当FN=0时,小滑块开始脱离斜面,此时,qvB=mgcosα
得: ![]()
(3)下滑过程中,只有重力做功,由动能定理得: ![]()
![]()
斜面的长度至少应是s ="1.2" m。

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】某同学利用如图所示的装置验证动能定理。固定并调整斜槽,使它的末端O点的切线水平,在水平地面上依次铺放好木板、白纸、复写纸。将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并根据落点位置测量出小球平抛的水平位移x。改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:
高度 H(h为单位长度) | h | 2h | 3h | 4h | 5h | 6h | 7h | 8h | 9h |
水平位移 x/cm | 5.5 | 9.1 | 11.7 | 14.2 | 15.9 | 17.6 | 19.0 | 20.6 | 21.7 |

(1)已知斜槽倾角为θ,小球与斜槽之间的动摩擦因数为μ,斜槽底端离地的高度为y,不计小球与水平槽之间的摩擦,小球从斜槽上滑下的过程中,动能定理若成立应满足的关系式是____________________;
(2)以H为横坐标,以__________为纵坐标,在坐标纸上描点作图,如图乙所示;

(3)由第(1)、(2)问,可以得出结论:_____________________________________________