题目内容
【题目】如图所示为某质点做直线运动的v—t图象。已知t0时刻质点的速度为v0,2t0时刻质点的速度为2v0图中OA与AB是关于A点中心对称的曲线。由此可求出的物理量有( )
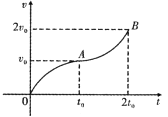
A. 0~t0时间内的位移
B. t0~2t0时间内的平均速度
C. 0~2t0时间内的位移
D. 2t0时刻的加速度
【答案】C
【解析】
A.对于速度时间图象,图线与坐标轴围成面积表示位移,0~t0时间内的图象是曲线且不知是何种线,故无法求解0~t0时间内的位移,故A错误;
B.对于速度时间图象,图线与坐标轴围成面积表示位移,t0~2t0时间内的图象是曲线且不知是何种线,故无法求解t0~2t0时间内的位移,则无法求解t0~2t0时间内的平均速度,故B错误;
C.图中OA与AB是关于A点中心对称的曲线,利用割补法可知图线围成面积等于连接OB,OB图象与坐标轴围成三角形面积,该面积可求,即可求0~2t0时间内的位移,故C正确;
D.对于速度-时间图象,速度的斜率表示加速度,但2t0时刻的斜率无法求解,即无法求解2t0时刻的加速度,故D错误;
故选C.

练习册系列答案
相关题目