题目内容
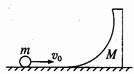
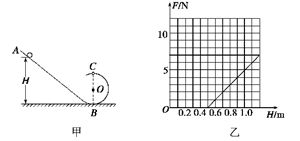
(18分)如右图所示,在竖直面内有一个光滑弧形轨道,其末端水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接。A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧。两滑块从弧形轨道上的某一高度由静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动恰能通过轨道最高点。已知圆形轨道的半径R=0.50m,滑块A的质量mA=0.16kg,滑块B的质量mB=0.04kg,两滑块开始下滑时距圆形轨道底端的高度h=0.80m,重力加速度g取10m/s2,空气阻力可忽略不计。

试求:(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小;
(2)滑块A被弹簧弹开时的速度大小;
(3)弹簧在将两滑块弹开的过程中释放的弹性势能。

试求:(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小;
(2)滑块A被弹簧弹开时的速度大小;
(3)弹簧在将两滑块弹开的过程中释放的弹性势能。
(1)4.0m/s(2)5.0 m/s(3)0.40J
(1)设滑块A和B运动到圆形轨道最低点速度为v0,对滑块A和B下滑到圆形轨道最低点的过程,根据动能定理,有
(mA+mB)gh=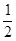 (mA+mBv02 ………………………………(2分)
(mA+mBv02 ………………………………(2分)
解得 v0="4.0m/s" ………………………………(2分)
(2)设滑块A恰能通过圆形轨道最高点时的速度大小为v,根据牛顿第二定律有 mAg=mAv2/R ………………………………(2分)
设滑块A在圆形轨道最低点被弹出时的速度为vA,对于滑块A从圆形轨道最低点运动到最高点的过程,根据机械能守恒定律,有
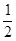 mAvA2=mAg?2R+
mAvA2=mAg?2R+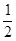 mAv2 ………………………………(2分)
mAv2 ………………………………(2分)
代入数据联立解得:vA="5.0" m/s ………………………………(2分)
(3)对于弹簧将两滑块弹开的过程,A、B两滑块所组成的系统水平方向动量守恒,设滑块B被弹出时的速度为vB,根据动量守恒定律,有
(mA+mB)v0=mA vA+ mBvB ………………………………(2分)
解得: vB=0 ………………………………(2分)
设弹簧将两滑块弹开的过程中释放的弹性势能为Ep,对于弹开两滑块的过程,根据机械能守恒定律,有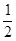 (mA+mB)v02 + Ep=
(mA+mB)v02 + Ep=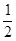 mAvA2 ………………………………(2分)
mAvA2 ………………………………(2分)
解得:Ep=0.40J ………………………………(2分)
(mA+mB)gh=
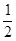 (mA+mBv02 ………………………………(2分)
(mA+mBv02 ………………………………(2分)解得 v0="4.0m/s" ………………………………(2分)
(2)设滑块A恰能通过圆形轨道最高点时的速度大小为v,根据牛顿第二定律有 mAg=mAv2/R ………………………………(2分)
设滑块A在圆形轨道最低点被弹出时的速度为vA,对于滑块A从圆形轨道最低点运动到最高点的过程,根据机械能守恒定律,有
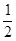 mAvA2=mAg?2R+
mAvA2=mAg?2R+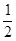 mAv2 ………………………………(2分)
mAv2 ………………………………(2分)代入数据联立解得:vA="5.0" m/s ………………………………(2分)
(3)对于弹簧将两滑块弹开的过程,A、B两滑块所组成的系统水平方向动量守恒,设滑块B被弹出时的速度为vB,根据动量守恒定律,有
(mA+mB)v0=mA vA+ mBvB ………………………………(2分)
解得: vB=0 ………………………………(2分)
设弹簧将两滑块弹开的过程中释放的弹性势能为Ep,对于弹开两滑块的过程,根据机械能守恒定律,有
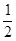 (mA+mB)v02 + Ep=
(mA+mB)v02 + Ep=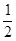 mAvA2 ………………………………(2分)
mAvA2 ………………………………(2分)解得:Ep=0.40J ………………………………(2分)

练习册系列答案
相关题目
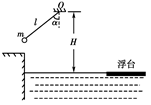

 ,A、B两物体与斜面的动摩擦因素均为
,A、B两物体与斜面的动摩擦因素均为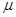 ,且最大的静摩擦力等于滑动摩擦力。现突然给A施一水平向右冲量I,A、B碰撞无机械能损失,滑块由水平面运动至斜面也不考虑转弯处的机械能损失。求
,且最大的静摩擦力等于滑动摩擦力。现突然给A施一水平向右冲量I,A、B碰撞无机械能损失,滑块由水平面运动至斜面也不考虑转弯处的机械能损失。求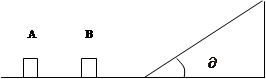
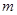 的小球以速度
的小球以速度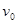 向槽运动,若开始时槽固定不动,求小球上升的高度(槽足够高);若槽不固定,则小球又上升多高?
向槽运动,若开始时槽固定不动,求小球上升的高度(槽足够高);若槽不固定,则小球又上升多高?