题目内容
16. 将质量分布均匀、重为G、半径为R的光滑圆球,用长度也为R的细绳拴在竖直墙上,求绳子对球的拉力FT和墙对球的作用力FN的大小.
将质量分布均匀、重为G、半径为R的光滑圆球,用长度也为R的细绳拴在竖直墙上,求绳子对球的拉力FT和墙对球的作用力FN的大小.
分析 圆球受重力、墙壁的弹力和绳子的拉力处于平衡状态,根据合成法,求出绳子的拉力和墙壁的弹力.
解答  解:F与竖直方向之间的夹角为θ:则sinθ=$\frac{R}{R+R}=\frac{1}{2}$,θ=30°
解:F与竖直方向之间的夹角为θ:则sinθ=$\frac{R}{R+R}=\frac{1}{2}$,θ=30°
圆球受力如图,根据合成法,知绳子拉力和墙壁弹力的合力与重力等值反向,运用几何关系得:
F=$\frac{G}{cos30°}=\frac{2\sqrt{3}G}{3}$
FN=Gtan30°=$\frac{\sqrt{3}}{3}$G
答:绳子对球的拉力为$\frac{2\sqrt{3}G}{3}$,墙对球的作用力的大小为$\frac{\sqrt{3}}{3}$G.
点评 物体处于共点力平衡时合力等于零,处理共点力平衡的方法有:合成法、正交分解法等.

练习册系列答案
相关题目
6. 如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )
如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )
 如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )
如图所示,木板长为l,板的A端放一质量为m的小物块,物块与板间的动摩擦因数为μ.开始时板水平,在绕O点缓慢转过一个小角度θ的过程中,若物块始终保持与板相对静止.对于这个过程中各力做功的情况,下列说法正确的是( )| A. | 摩擦力对物块所做的功为mglsinθ(1-cosθ) | |
| B. | 弹力对物块所做的功为mglsinθcosθ | |
| C. | 木板对物块所做的功为mglsinθ | |
| D. | 合力对物块所做的功为mglcosθ |
1.下列单位符号与“Pa”等价的有( )
| A. | N/m2 | B. | J/m3 | C. | kg/(s2•m) | D. | W•s/m3 |
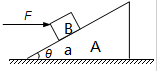 斜面体A质量为m0,倾角为θ,敦在水平地面上.一质量为m的物体B放在斜面体上.用水平恒力F作用于B,使A和B一起以相同的加速度a沿水平地面运动,如图所示,求地面对斜面体摩擦力的大小.
斜面体A质量为m0,倾角为θ,敦在水平地面上.一质量为m的物体B放在斜面体上.用水平恒力F作用于B,使A和B一起以相同的加速度a沿水平地面运动,如图所示,求地面对斜面体摩擦力的大小.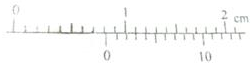 如图所示,若用20分度的游标卡尺测量遮光条的宽度,其读数为8.15mm.
如图所示,若用20分度的游标卡尺测量遮光条的宽度,其读数为8.15mm.