题目内容
9.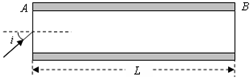 一条圆柱形的光导纤维长度为L=1200m,它的玻璃芯外层材料的折射率为n1=$\frac{\sqrt{6}}{2}$,它的内层玻璃芯材料的折射率为n2=$\frac{3}{2}$,将其置于空气中,如图所示.求:
一条圆柱形的光导纤维长度为L=1200m,它的玻璃芯外层材料的折射率为n1=$\frac{\sqrt{6}}{2}$,它的内层玻璃芯材料的折射率为n2=$\frac{3}{2}$,将其置于空气中,如图所示.求:(1)若从A端射入的光线能在玻璃纤维中发生全反射,最后从B端射出,光在A端面上入射角的最大值.
(2)若一束光在纤维中恰好发生全反射,由A端射入到B端射出经历的时间为多少?
(3)若n2=$\frac{3}{2}$不变,要使从A端射入的光线不论入射角多大,都能在玻璃纤维中发生全反射,而从B端射出,玻璃纤维外层材料的折射率的取值范围应为多大?
分析 (1)光线在光纤侧面恰好发生全反射时,入射角等于临界角C,光在A面上入射角最大,先根据公式sinC=$\frac{1}{n}$,求出临界角C,再由几何关系求出光线在A端面的折射角,即可由折射率公式求解入射角的最大值.
(2)由数学知识求出从左端射入到右端射出光线通过的路程x.光在光纤中的传播速度为v=$\frac{c}{n}$,由t=$\frac{x}{v}$求解时间.或求出光在沿纤维轴线方向上的速度分量求解时间.
(3)当入射角θ1=90°时,折射率最小,从而即可求解.
解答 解: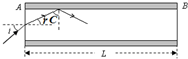
(1)如图所示,由题意可知由于n2>n1,因此只要从端面A进入的光线射在内外层界面处的入射角θ大于等于其临界角C,从A端射入的光线便能在玻璃纤维中发生全反射,最后从B端射出.由几何关系可知,θ取最小值C时,端面A的折射角r和入射角i有最大值.
由光的折射规律可知:
n2=$\frac{sini}{sinr}$…①
内层玻璃芯材料相对外层材料的折射率为:$n=\frac{{n}_{2}}{{n}_{1}}$…②
内层玻璃芯材料相对外层材料的全反射临界角为C,则:sinC=$\frac{1}{n}$…③
由几何关系:r=90°-C…④
解①②③④得:i=60°
(2)光在玻璃纤维芯中传播速度为v=$\frac{c}{{n}_{2}}$(c为真空中光速)…⑤
沿光纤轴向速度分量为v1=vsinC…⑥
所用时间为t=$\frac{L}{{v}_{1}}$…⑦
解③⑤⑥⑦得t=3$\sqrt{6}$×10-6s
(3)若端面A处入射角取最大为i=90°时,都能在玻璃纤维中发生全反射,
而从B端射出.则从A端射入的光线不论入射角多大,都能在玻璃纤维中发生全反射,而从B端射出.因此,当n2=$\frac{3}{2}$不变,i=90°时,解①②③④得,n1=$\frac{\sqrt{5}}{2}$
所以1≤n1≤$\frac{\sqrt{5}}{2}$
答:(1)若从A端射入的光线能在玻璃纤维中发生全反射,最后从B端射出,光在A端面上入射角的最大值60°.
(2)若一束光在纤维中恰好发生全反射,由A端射入到B端射出经历的时间为3$\sqrt{6}$×10-6s;
(3)若n2=$\frac{3}{2}$不变,要使从A端射入的光线不论入射角多大,都能在玻璃纤维中发生全反射,而从B端射出,玻璃纤维外层材料的折射率的取值范围应为1≤n1≤$\frac{\sqrt{5}}{2}$.
点评 是对于几何光学问题,一定要画出光路图,并根据题意找出临界角与其他角度的关系,再结合相应的规律解题.

 阅读快车系列答案
阅读快车系列答案| A. | “天宫一号”飞行器的高度要略调高一点 | |
| B. | 地球赤道上物体的重力会略变大 | |
| C. | 同步卫星的高度要略调低一点 | |
| D. | 地球的第一宇宙速度将略变小 |
| A. | 第n个△t 内的位移 | B. | 物体运动的加速度 | ||
| C. | n△t 内物体的位移 | D. | 第一个△t 内的平均速度 |
 如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则( )
如图所示,两艘飞船A、B沿同一直线同向飞行,相对地面的速度均为v(v 接近光速c). 地面上测得它们相距为L,则( )| A. | A测得两飞船间的距离大于L | |
| B. | B测得两飞船间的距离小于L | |
| C. | 当B向A发出一束光信号,A测得该信号的速度为c | |
| D. | 当B向A发出一束光信号,A测得该信号的速度为cv |

| A. | 绳拉牛的力与牛拉绳的力是一对平衡力 | |
| B. | 绳拉牛的力与地面对牛的摩擦力是一对作用力与反作用力 | |
| C. | 小孩拉牛的力等于牛拉小孩的力 | |
| D. | 绳拉牛的力小于地面对牛的摩擦力 |
下表是该同学记录的数据:
| 代表符号 | L0 | L1 | L2 | L3 |
| 刻度数值/cm | 5.70 | 7.40 | 9.15 | 10.95 |
(2)已知重力加速度g,则计算该弹簧的劲度系数的表达式k=$\frac{mg}{△L}$.
(3)若m=50g,g=9.8m/s2可求弹簧的劲度系数k=28N/m.
 某小型发电站发电机输出的交流电压为500V,输出的最大电功率为50kW,用电阻为3Ω的输电线向远处送电,要求输电线上损失功率为输电功率的0.6%,则发电站要安装一升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器)求:
某小型发电站发电机输出的交流电压为500V,输出的最大电功率为50kW,用电阻为3Ω的输电线向远处送电,要求输电线上损失功率为输电功率的0.6%,则发电站要安装一升压变压器,到达用户再用降压变压器变为220V供用户使用(两个变压器均为理想变压器)求: 如图所示的电路中,电源电压保持不变,闭合开关,当滑动变阻器的滑片P向右移动时,电流表A的示数将变小,(填“变小”、“不变”或“变大”),电压表V与电压表V2示数的差值将不变.(填“变小”、“不变”或“变大”)
如图所示的电路中,电源电压保持不变,闭合开关,当滑动变阻器的滑片P向右移动时,电流表A的示数将变小,(填“变小”、“不变”或“变大”),电压表V与电压表V2示数的差值将不变.(填“变小”、“不变”或“变大”)