��Ŀ����
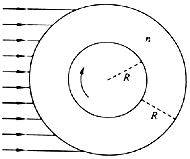
����Ŀ����ͼ��ʾ��װ����ֱ���ã��϶��ǹ⻬ϸԲ��Χ�ɵ�Բ�ܹ����һ���֣��뾶ΪR��Բ���ھ�����R��������¶˸����������ֲڵ�б�棬б����ϸԲ��������C��D���㣬б����ˮƽ��н�Ϊ53�㣬����б���¶���뾶Ϊ0.5R��Բ�ι⻬������ӣ���������E��F���㣮��һ����m=1kg�Ļ��飨�����С��С�ڹܵ��ھ������ӹܵ�����ߵ�A��ֹ�ͷŸû��飬����ӹܵ����£������ֲڵ�б��Ķ�Ħ��������=0.5����g=10m/s2 �� sin53��=0.8��cos53��=0.6������ ��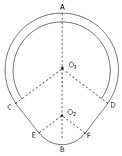
A.�ͷź��ڹ�����˶��ﵽ����ߵ�߳�O1��0.6R
B.���龭����͵�B��ѹ����СΪ18N
C.��������ܾ���D��4��
D.�������ջ�ͣ��B��
���𰸡�A,B
���������⣺A����CE=FD=L���ɼ���֪ʶ�ɵ� L=0.5Rtan53��= ![]() R
R
���ͷź��ڹ�����˶��ﵽ����ߵ�߳�O1��h���ɶ��ܶ����ã�mg��R��h����2��mgcos53��L=0����� h=0.6R�����ͷź��ڹ�����˶��ﵽ����ߵ�߳�O1��0.6R����A��ȷ��
BD��������б���ϻ���ʱ��е�ܲ��ϼ��٣����ջ�����EF�������˶�����E��F�Ĺ��̣��ɻ�е���غ㶨�ɵã�
mg0.5R��1��cos53�㣩= ![]() ��0
��0
��B�㣬��ţ�ٵڶ����ɵ� N��mg=m ![]()
������� N=18N����ţ�ٵ������ɵã����龭����͵�B��ѹ����Сֵ N��=N=18N����B��ȷ��D����
C���軬��������б���ϻ��е���·��ΪS�����������̣���A��E��F�Ĺ��̣������ö��ܶ�����
mg��R+Rcos53��+Lsin53�㣩����mgcos53��S=0����� S= ![]() R
R
��Ϊ ![]() =
= ![]() =
= ![]() ������ S=��5+
������ S=��5+ ![]() ��2L=5��2L+
��2L=5��2L+ ![]() L�����Ի�������ܾ���D��5�Σ���C����
L�����Ի�������ܾ���D��5�Σ���C����
��ѡ��AB
�����㾫�������ڱ��⿼����������Ͷ��ܶ������ۺ�Ӧ�ã���Ҫ�˽�����������ָ��Բ�ģ��������ļ��ٶȣ�������ֻ�ı����ٶȵķ����ı��ٶȵĴ�С���������Ǹ�������Ч��������.�ڷ�����Բ���˶����ʵ��������ʱ��ǧ������������֮��������һ����������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ��ܵó���ȷ�𰸣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�