题目内容
【题目】设太阳系中某行星半径为R,被厚度也为R的、折射率n= ![]() 的均质大气层所包围,如图所示,已知该行星的自转轴和黄道面垂直,试求:
的均质大气层所包围,如图所示,已知该行星的自转轴和黄道面垂直,试求:
①在该行星上看到日落时,阳光进入大气层的折射角;
②若该行星自转周期T=24h,忽略其公转的影响,则该行星上白天的时间为多长?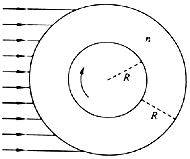
【答案】解:①如图,看到日落时,折射光和行星表面相切,设为B点,则对Rt△ABO,有: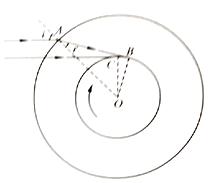
sinr= ![]()
代入已知条件 BO=R和AO=R+R得:
折射角 r=30°
②在A点,由折射定律有![]() =n
=n
代入 n= ![]() ,得 i=45°
,得 i=45°
如果没有大气层,看到日落时,平行的阳光直射,相切于C点,因大气存在,行星延迟日落对应的自转角度为∠COB.
由几何关系可知,∠COB=i﹣r=15°
延迟的时间 t= ![]() T=
T= ![]() T=1h
T=1h
同理,太阳升起时,也会因大气折射提早时间t
所以该行星上白天的时间为 ![]() +t+t=14h
+t+t=14h
答:①在该行星上看到日落时,阳光进入大气层的折射角是30°;
②若该行星自转周期T=24h,忽略其公转的影响,则该行星上白天的时间为14h.
【解析】①在该行星上看到日落时,折射光与行星表面相切,画出光路图,根据几何知识求阳光进入大气层的折射角;②根据折射定律求出入射角,结合几何关系和行星运动规律求解.
【考点精析】认真审题,首先需要了解光的折射(光由一种介质射入另一种介质时,在两种介质的界面上将发生光的传播方向改变的现象叫光的折射).

练习册系列答案
相关题目