题目内容
11.一水平放置的圆盘绕过其圆心的竖直轴匀速转动.盘边缘上固定一竖直的挡光片.盘转动时挡光片从一光电数字计时器的光电门的狭缝中经过,如图1 所示.图2为光电数字计时器的示意图.光源A中射出的光可照到B中的接收器上.若A、B间的光路被遮断,显示器C上可显示出光线被遮住的时间.已测得挡光片的宽度为10.00mm,圆盘直径直径为30.00cm,若光电数字计时器所显示的时间为50.0ms.则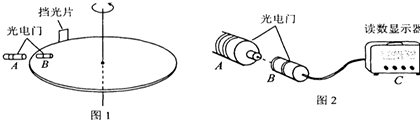
(1)圆盘转动的线速度为0.2m/s.
(2)圆盘转动的角速度为0.667rad/s(此项结果保留3位有效数字)
分析 (1)由v=$\frac{D}{t}$求出圆盘转动的线速度.
(2)由v=ωr,求出角速度ω.
解答 解:(1)圆盘转动的线速度为:
v=$\frac{D}{t}$=$\frac{10.00×1{0}^{-3}}{50.0×1{0}^{-3}}=0.2$m/s
(2)由v=ωr得角速度为:
ω=$\frac{v}{r}$
又r=$\frac{d}{2}$
联立,代入解得:
ω=$\frac{0.2}{\frac{30.00×1{0}^{-2}}{2}}=0.667$rad/s
故答案为:(1)0.2;(2)0.667
点评 掌握圆周运动的线速度与角速度的关系v=ωr是解答该题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.图(1)为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置在x=1.0m处的质点,Q是平衡位置在x=6.0m处的质点.图(2)为质点Q的振动图象,下列说法正确的是( )
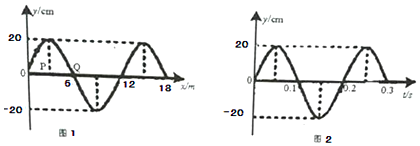

| A. | 这列简谐横波的波速为60m/s | |
| B. | 在t=0.10s时,质点P的运动方向与y轴正方向相同 | |
| C. | 在t=0.10s时,质点Q向y轴负方向运动 | |
| D. | 从t=0.10s到t=0.20s,质点Q通过的路程为20cm | |
| E. | 质点Q简谐运动的表达式为y=0.20sin$\frac{20π}{3}$t(cm) |
2. 如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
 如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )
如图所示,质量相等的A、B两个球,原来在光滑水平面上沿同一直线相向做匀速直线运动,A球的速度是6m/s,B球的速度是-2m/s,不久A、B两球发生了对心碰撞.对于该碰撞之后的A、B两球的速度可能值,某实验小组的同学们做了很多种猜测,下面的猜测结果一定无法实现的是( )| A. | vA′=-2 m/s,vB′=6 m/s | B. | vA′=2 m/s,vB′=2 m/s | ||
| C. | vA′=1 m/s,vB′=3 m/s | D. | vA′=-3 m/s,vB′=7 m/s |
19.一质量为2kg的物体在5个共点力作用下做匀速直线运动.现撤去其中一个大小为10N的力,其余的力大小和方向均保持不变.下列关于此后该物体运动的说法中,正确的是( )
| A. | 可能做匀减速直线运动,加速度大小为5 m/s2 | |
| B. | 可能做匀速圆周运动,向心加速度大小为5 m/s2 | |
| C. | 可能做匀变速曲线运动,加速度大小为5 m/s2 | |
| D. | 一定做匀变速直线运动,加速度大小为5 m/s2 |
3.有一悬线场为l的单摆,其摆的外壳为一个有一定质量的金属空心球,球底有小孔,球内盛满水,在摆动过程中,水从小孔慢慢流出,从水开始流到水流完的过程,此摆的周期变化是( )
| A. | 由于悬线长l和重力加速度g不变,所以周期不变 | |
| B. | 由于水不断外流,周期不断变大 | |
| C. | 周期先变大,后变小 | |
| D. | 周期先变小,后变大 |
1.以下说法中正确的是( )
| A. | 光波是概率波,物质波不是概率波 | |
| B. | 实物粒子不具有波动性 | |
| C. | 实物粒子也具有波动性,只是不明显 | |
| D. | 光的波动性是光子之间相互作用引起的 |


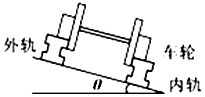 铁路在弯道处的内外轨道高低是不同的,已知内外轨道对水平面倾角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则火车不挤压内外轨道,若速度大于$\sqrt{gRtanθ}$则火车挤压外轨道,若速度小于$\sqrt{gRtanθ}$则火车挤压内轨道.(填“内”或“外”)
铁路在弯道处的内外轨道高低是不同的,已知内外轨道对水平面倾角为θ,如图所示,弯道处的圆弧半径为R,若质量为m的火车转弯时速度等于$\sqrt{gRtanθ}$,则火车不挤压内外轨道,若速度大于$\sqrt{gRtanθ}$则火车挤压外轨道,若速度小于$\sqrt{gRtanθ}$则火车挤压内轨道.(填“内”或“外”)