Question

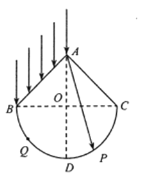
【题目】在光滑水平桌面中央固定一边长为0.3m的小正三棱柱abc俯视如图．长度为L=1m的细线，一端固定在a点，另一端拴住一个质量为m=0.5kg、不计大小的小球．初始时刻，把细线拉直在ca的延长线上，并给小球以v0=2m/s且垂直于细线方向的水平速度，由于光滑棱柱的存在，细线逐渐缠绕在棱柱上（不计细线与三棱柱碰撞过程中的能量损失）．已知细线所能承受的最大张力为7N，则下列说法中正确的是：

A.细线断裂之前，小球角速度的大小保持不变

B.细线断裂之前，小球的速度逐渐减小

C.细线断裂之前，小球运动的总时间为0.7π（s）

D.细线断裂之前，小球运动的位移大小为0.9（m）

Answer 1

【答案】CD

【解析】

试题A、B细线断裂之前，绳子拉力与速度垂直，不做功，不改变小球的速度大小，故小球的速度大小保持不变，由圆周运动的速度与角速度的关系式v=r，随r减小，小球角速度增大，故A、B错误；绳子刚断裂时，拉力大小为7N，由F=m，解得此时的半径为r=m，由于小球每转120°半径减小0.3m，则知小球刚好转过一周，细线断裂，则小球运动的总时间为t=，其中r1=1m，r2=0.7m，r3=0.4m，v0=2m/s，解得t=0.7π（s），故C正确；小球每转120°半径减小0.3m，细线断裂之前，小球运动的位移大小为0.9m，故D正确．故选CD