题目内容
13.摩托车以v1=8m/s的速度沿平直公路行驶,突然,驾驶员发现正前方s处有一辆汽车正以v2=6m/s的速度开始做匀减速运动,加速度大小为a2=1m/s2.求:(1)汽车从此时开始,刹车至停下的时间和通过的位移;
(2)当s=14m时,摩托车为避免与汽车相撞,刹车时的加速度至少是多少?
(3)当s=5m时,摩托车为避免与汽车相撞,刹车时的加速度至少是多少?
分析 (1)根据速度时间公式求出汽车刹车至停下的时间,结合平均速度推论求出通过的位移.
(2、3)当两车同向运动时,为了避免发生碰撞,摩托车在减速的过程中,当两车的速度相等时,应满足的位移关系是:x摩托车=x汽车+s,然后根据匀速运动的公式和匀减速运动的位移公式,即可求解.
解答 解:(1)汽车刹车至停下的时间t=$\frac{0-{v}_{2}}{{a}_{2}}=\frac{-6}{-1}s=6s$,
通过的位移x=$\frac{{v}_{2}}{2}t=\frac{6}{2}×6m=18m$.
(2)设摩托车经过时间t1与汽车达到共同速度,有:
v1-a1t1=v2-a2t1
此段时间内摩托车的位移:
x1=v1t1-$\frac{1}{2}{a}_{1}{{t}_{1}}^{2}$
汽车的位移:
x2=v2t1-$\frac{1}{2}{a}_{2}{{t}_{1}}^{2}$
如果速度相同时恰好不相撞,此时对应的加速度a1最小,则由位置关系:
x1=x2+s
代入数值可得:${a}_{1}=\frac{8}{7}m/{s}^{2}$.
t1=14s>6s 不合实际,即一定不存在追上时速度相等的情况,即追上前一定是摩托车快;
故临界情况是在汽车停止位置相遇,故:
x1=v1t1-$\frac{1}{2}{a}_{1}{{t}_{1}}^{2}$
x2=18m
x1=x2+s
联立解得:
a1=1m/s2
(3)当S=5m时,摩托车为避免与汽车相撞,有:
设摩托车经过时间t2与汽车达到共同速度,有:
v1-a1t2=v2-a2t2
此段时间内摩托车的位移:
x1=v1t2-$\frac{1}{2}{a}_{1}{{t}_{2}}^{2}$
汽车的位移:
x2=v2t2-$\frac{1}{2}{a}_{2}{{t}_{2}}^{2}$
如果速度相同时恰好不相撞,此时对应的加速度a1最小,则由位置关系:
x1=x2+s
代入数值可得:
a1=$\frac{8}{7}m/{s}^{2}$
t1=5s<6s 符合实际
答:(1)刹车至停下的时间为6s,通过的位移为18m.
(2)当S=14m时,摩托车为避免与汽车相撞,刹车时的加速度至少是1m/s2;
(3)当S=5m时,摩托车为避免与汽车相撞,刹车时的加速度至少是$\frac{8}{7}$m/s2.
点评 解答此种追击问题的题目,要抓住恰好追上时,两车在同一时刻出现在同一个位置上;然后结合两车运动的规律,如:加速、减速、匀速等,列出相应的公式,进行解题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 北京时间2013年12月2日凌晨,中国在西昌卫星发射中心成功将嫦娥三号月球探测器送入太空.如图所示,嫦娥三号在A点经制动进入环月圆轨道Ⅰ,然后再次在A点制动将轨道Ⅰ变为椭圆轨道Ⅱ,使其近月点B点距月球表面大约15公里.下列说法正确的是( )
北京时间2013年12月2日凌晨,中国在西昌卫星发射中心成功将嫦娥三号月球探测器送入太空.如图所示,嫦娥三号在A点经制动进入环月圆轨道Ⅰ,然后再次在A点制动将轨道Ⅰ变为椭圆轨道Ⅱ,使其近月点B点距月球表面大约15公里.下列说法正确的是( )| A. | 沿轨道Ⅰ运动至A时,需制动减速才能进入轨道ⅡB | |
| B. | 嫦娥三号在轨道Ⅰ上的速率小于在轨道Ⅱ上的速率 | |
| C. | 嫦娥三号在轨道Ⅰ上的速度大于月球的第一宇宙速度 | |
| D. | 嫦娥三号在轨道Ⅱ上A点的加速度大于在轨道Ⅰ上A点的加速度 |
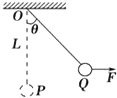 一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平拉力F作用下从平衡位置P点很缓慢地移到Q点,如图所示,则力F做功为( )
一质量为m的小球,用长为L的轻绳悬挂于O点,小球在水平拉力F作用下从平衡位置P点很缓慢地移到Q点,如图所示,则力F做功为( )| A. | mgLcosθ | B. | mgL(1-cosθ) | C. | FLsinθ | D. | FLcosθ |
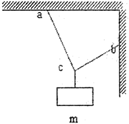 用三根轻绳将质量为m的物块悬挂在空中,如图所示已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )
用三根轻绳将质量为m的物块悬挂在空中,如图所示已知ac和bc与竖直方向的夹角分别为30°和60°,则ac绳和bc绳中的拉力分别为( )| A. | $\frac{{\sqrt{3}}}{4}$mg,$\frac{1}{2}$mg | B. | $\frac{{\sqrt{3}}}{2}$mg,$\frac{1}{2}$mg | C. | $\frac{1}{2}$mg,$\frac{{\sqrt{3}}}{4}$mg | D. | $\frac{1}{2}$mg,$\frac{{\sqrt{4}}}{4}$mg |
 如图所示,通电直导线ab位于两平行导线横截面M、N的连线的中垂线上,o为MN连线的中点,当平行导线M、N通以同向等值电流I时,以下说法中正确的是( )
如图所示,通电直导线ab位于两平行导线横截面M、N的连线的中垂线上,o为MN连线的中点,当平行导线M、N通以同向等值电流I时,以下说法中正确的是( )| A. | 通电导线M、N在o点产生的合磁场方向向下 | |
| B. | 通电导线M、N在o点上方产生的合磁场方向向左 | |
| C. | ab受到磁场力后将绕o在纸平面内逆时针旋转 | |
| D. | ab受到磁场力后a端向纸外,b端向纸里旋转 |
| A. | 做斜抛运动的铅球 | B. | 沿竖直方向下落的物体 | ||
| C. | 起重机将重物匀速吊起 | D. | 沿光滑竖直圆轨道匀速运动的小球 |
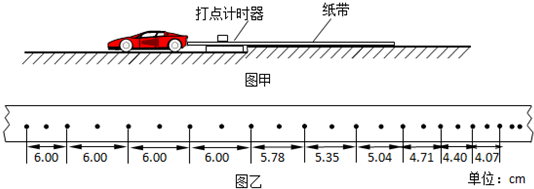
| A. | 小球在这4s内的平均速度是2.5 m/s | |
| B. | 小球在第3、第4两秒内的平均速度是3.5 m/s | |
| C. | 小球在第3 s末的瞬时速度是3.5 m/s | |
| D. | 小球的初速度为零 |
 物体以一定的初速度从A点冲上固定的光滑的斜面,到达斜面最高点C时速度恰好为零,如图所示.已知物体运动到斜面长度$\frac{3}{4}$处的B点时,所用时间为t,求物体从B运动到C所用的时间.
物体以一定的初速度从A点冲上固定的光滑的斜面,到达斜面最高点C时速度恰好为零,如图所示.已知物体运动到斜面长度$\frac{3}{4}$处的B点时,所用时间为t,求物体从B运动到C所用的时间.