题目内容
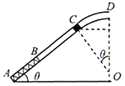
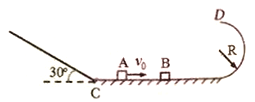
【题目】如图所示，倾角为30°的粗糙斜面与光滑水平轨道通过一小段圆弧在C点相接，水平轨道的右侧与半径为R=0.32m的光滑竖直半圆形轨道相连。质量为0.5kg的物体B静止在水平轨道上，一质量为0.1kg的A物体以v0=16m/s的速度与B发生正碰，结果B恰好能通过半圆形轨道的最高点。A、B均可看成质点，除第一次碰撞外，不考虑A、B间其他的相互作用，已知A与斜面间的动摩擦因数为μ=
，取g=10m/s2。求：
(1)碰撞过程中A对B的冲量大小
(2)A从第一次冲上斜面到离开斜面的时间
【答案】（1）2Ns（2）1.5s
【解析】
（1）利用牛顿第二定律与动能定理求出B碰后的速度，然后利用动量定理进行求解；
（2）利用动量守恒定律求出A碰后的速度，然后利用牛顿第二定律结合运动学公式进行求解即可；
（1）B恰好能通过最高点，故在最高点有：
设A、B碰后的B速度为vB，则B从碰后到B运动到D点的过程中有：
代入数据联解得：
故A对B的冲量大小为：
；
（2）A、B碰撞过程中动量守恒，以
方向为正，则有：
代入数据，解得：
，负号说明其方向与方向相反
因此A以
的速度冲上斜面，A沿斜面向上运动的加速度大小为：
A沿斜面向上运动的时间为：
A沿斜面向上运动的距离为：
A沿斜面向下运动的加速度大小为： 
A沿斜面向下运动的过程中有：
，代入数据解得：
故A从第一次冲上斜面到离开斜面的时间为：
。
练习册系列答案
相关题目
