题目内容
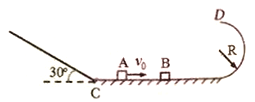
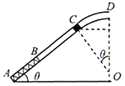
【题目】如图所示，竖直平面内倾角为θ＝37°的直管道AC和光滑的圆弧管道CD相切于C点，直管道AC的底端固定一轻弹簧，另一端位于直管道上B处，弹簧处于自然状态，原长为2R．圆弧管道的半径为5R，D端水平。质量为m的小滑块（可视为质点）自C点以初速度
下滑，最低到达E点（图中未画出），随后小滑块沿管道被弹回，恰能通过圆弧管道的最高点，小滑块与直管道AC间的动摩擦因数为μ＝0.5，BC＝5R，重力加速度为g，sin37°＝0.6，cos37＝0.8．求：
（1）小滑块第一次运动到B点时的速度大小v1；
（2）小滑块第二次运动到B点时的速度大小v2；
（3）小滑块在最低点E的弹性势能Ep。
【答案】（1）
；（2）
；（3）
【解析】
（1）第一次达到B的过程由牛顿第二定律得：mgsinθ﹣μmgcosθ＝ma
由速度位移的关系式得：vB2﹣vC2＝2axBC
解得：
（2）小球恰能通过最高点，则有：vD＝0
小球返回B向上移动的过程中由动能定理得：
﹣mgxBCsinθ﹣5mgR（1﹣cosθ）﹣μmgxBCcosθ＝
解得：
（3）设弹簧的最大压缩量为x，从开始运动到第二次到达B点的过程，由动能定理得：
mgxBCsinθ﹣μmg（xBC+2x）cosθ＝
解得：
由能量守恒有：EP＝
+mgxsinθ+μmgxcosθ
解得：EP＝
mgR
练习册系列答案
相关题目
