题目内容
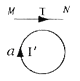
【题目】某空间站在半径为R的圆形轨道上运行,周期为T:另有一飞船在半径为r的圆形轨道上运行,飞船与空间站的绕行方向相同。当空间站运行到A点时,飞船恰好运行到B点,A、B与地心连线相互垂直,此时飞船经极短时间的点火加速,使其轨道的近地点为B、远地点与空间站的轨道相切于C点,如图所示。当飞船第一次到达C点时,恰好与空间站相遇。飞船上有一弹簧秤悬挂一物体。由以上信息可判定:

A. 某空间站的动能小于飞船在半径为r的圆形轨道上运行时的动能
B. 当飞船与空间站相遇时,空间站的加速度大于飞船的加速度
C. 飞船在从B点运动到C点的过程中,弹簧秤的示数逐渐变小(不包括点火加速阶段)
D. 空间站的圆形轨道半径R与飞船的圆形轨道半径r的关系满足:r=(![]() )R
)R
【答案】D
【解析】
根据万有引力提供向心力能判断二者圆周运动的线速度大小的关系,但是由于二者质量未知,故无法判断动能的关系;根据牛顿第二定律可知加速度与距离有关,从而判断二者在同一点时的加速度大小关系;飞船飞行过程中处于完全失重状态,所以弹簧秤没有示数;根据开普勒第三定律进行判断即可;
A、当空间站和飞船均做圆周运动时,其万有引力提供向心力,即![]()
则线速度大小为:![]() ,由于空间站的半径大于飞船的半径,故空间站的速度的大小小于飞船的速度大小,由于二者的质量关系未知,故根据动能的公式
,由于空间站的半径大于飞船的半径,故空间站的速度的大小小于飞船的速度大小,由于二者的质量关系未知,故根据动能的公式![]() 无法判断二者的动能大小关系,故选项A错误;
无法判断二者的动能大小关系,故选项A错误;
B、当飞船与空间站相遇时,根据牛顿第二定律有:![]() ,即
,即![]() ,可知二者相遇时其加速度的大小相等,故选项B错误;
,可知二者相遇时其加速度的大小相等,故选项B错误;
C. 飞船在从B点运动到C点的过程中,万有引力为合力,在飞行过程中处于完全失重状态,弹簧秤没有示数,故选项C错误;
D、设飞船椭圆轨道的周期为![]() ,则根据开普勒第三定律可知:
,则根据开普勒第三定律可知: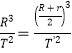
由题可知:![]() ,联立可以得到:
,联立可以得到:![]() ,故选项D正确。
,故选项D正确。

练习册系列答案
相关题目