题目内容
 如图所示,边长L=0.20m的正方形导线框ABCD由粗细均匀的同种材料制成,正方形导线框每边的电阻R0=1.0Ω,金属棒MN与正方形导线框的对角线长度恰好相等,金属棒MN的电阻r=0.20Ω.导线框放置在匀强磁场中,磁场的磁感应强度B=0.50T,方向垂直导线框所在平面向里.金属棒MN与导线框接触良好,且与导线框对角线BD垂直放置在导线框上,金属棒上的中点始终在BD连线上.若金属棒以v=4.0m/s的速度向右匀速运动,当金属棒运动至AC位置时,求:
如图所示,边长L=0.20m的正方形导线框ABCD由粗细均匀的同种材料制成,正方形导线框每边的电阻R0=1.0Ω,金属棒MN与正方形导线框的对角线长度恰好相等,金属棒MN的电阻r=0.20Ω.导线框放置在匀强磁场中,磁场的磁感应强度B=0.50T,方向垂直导线框所在平面向里.金属棒MN与导线框接触良好,且与导线框对角线BD垂直放置在导线框上,金属棒上的中点始终在BD连线上.若金属棒以v=4.0m/s的速度向右匀速运动,当金属棒运动至AC位置时,求:(1)金属棒产生的电动势大小;
(2)金属棒MN上通过的电流大小和方向;
(3)导线框消耗的电功率.
分析:(1)当金属棒运动至AC位置时,有效切割长度等于正方形对角线的长度.由公式E=BLv求解感应电动势的大小.
(2)导线框左、右两侧电阻并联,求出并联电阻,由闭合电路欧姆定律求解金属棒MN上通过的电流大小,由右手定则判断电流的方向.
(3)根据功率求解导线框消耗的电功率.
(2)导线框左、右两侧电阻并联,求出并联电阻,由闭合电路欧姆定律求解金属棒MN上通过的电流大小,由右手定则判断电流的方向.
(3)根据功率求解导线框消耗的电功率.
解答:解:
(1)金属棒产生的电动势大小为:
E=
BLv=0.4
V≈0.57V.
(2)金属棒运动到AC位置时,导线框左、右两侧电阻并联,其并联电阻大小为
R并=
?2R0=1.0Ω,
根据闭合电路欧姆定律 I=
≈0.48A,
根据右手定则判定,电流方向从N到M.
(3)导线框的功率为:P框=I2R并≈0.23W.
答:
(1)金属棒产生的电动势大小为0.57V.
(2)金属棒MN上通过的电流大小是0.48A,方向从N到M.
(3)导线框消耗的电功率是0.23W.
(1)金属棒产生的电动势大小为:
E=
| 2 |
| 2 |
(2)金属棒运动到AC位置时,导线框左、右两侧电阻并联,其并联电阻大小为
R并=
| 1 |
| 2 |
根据闭合电路欧姆定律 I=
| E |
| E井+r |
根据右手定则判定,电流方向从N到M.
(3)导线框的功率为:P框=I2R并≈0.23W.
答:
(1)金属棒产生的电动势大小为0.57V.
(2)金属棒MN上通过的电流大小是0.48A,方向从N到M.
(3)导线框消耗的电功率是0.23W.
点评:本题是电磁感应中电路问题,确定哪部分电路是电源,哪部分电路是外电路是基础,也可以作出等效电路.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 如图所示,边长L=0.20m的正方形导线框ABCD由粗细均匀的同种材料制成,正方形导线框每边的电阻R0=1.0Ω,金属棒MN与正方形导线框的对角线长度恰好相等,金属棒MN的电阻r=0.20Ω.导线框放置在匀强磁场中,磁场的磁感应强度B=0.50T,方向垂直导线框所在平面向里.金属棒MN与导线框接触良好,且与导线框对角线BD垂直放置在导线框上,金属棒的中点始终在BD连线上.若金属棒以v=4.0m/s的速度向右匀速运动.求(计算结果保留两位有效数字):
如图所示,边长L=0.20m的正方形导线框ABCD由粗细均匀的同种材料制成,正方形导线框每边的电阻R0=1.0Ω,金属棒MN与正方形导线框的对角线长度恰好相等,金属棒MN的电阻r=0.20Ω.导线框放置在匀强磁场中,磁场的磁感应强度B=0.50T,方向垂直导线框所在平面向里.金属棒MN与导线框接触良好,且与导线框对角线BD垂直放置在导线框上,金属棒的中点始终在BD连线上.若金属棒以v=4.0m/s的速度向右匀速运动.求(计算结果保留两位有效数字):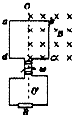 (2012?马鞍山模拟)如图所示,边长L=0.2m的正方形线圈abcd,其匝数n=lO,总电阻r=2Ω,外电路的电阻R=8Ω,ab边的中点和cd边的中点的连线00′恰好位于匀强磁场的边界线上,磁场的磁感应强度B=1T,若线圈从图示位置开始计时,以角速度ω=2rad/s绕00′轴匀速转动.则以下判断中正确的是( )
(2012?马鞍山模拟)如图所示,边长L=0.2m的正方形线圈abcd,其匝数n=lO,总电阻r=2Ω,外电路的电阻R=8Ω,ab边的中点和cd边的中点的连线00′恰好位于匀强磁场的边界线上,磁场的磁感应强度B=1T,若线圈从图示位置开始计时,以角速度ω=2rad/s绕00′轴匀速转动.则以下判断中正确的是( )
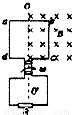
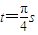 时刻,磁场穿过线圈的磁通量最大
时刻,磁场穿过线圈的磁通量最大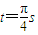 时刻,通过电阻R的电量q=0.02C
时刻,通过电阻R的电量q=0.02C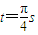 时刻,电阻R上产生的热量为Q=3.2π×10-4J
时刻,电阻R上产生的热量为Q=3.2π×10-4J