题目内容
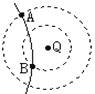
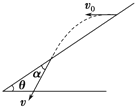
【题目】如图所示,从倾角为θ的足够长的斜面的顶端,先后将同一小球以不同的初速度水平向左抛出,第一次初速度为v1,球落到斜面上前一瞬间的速度方向与斜面夹角为α1,落点与抛出点间的距离为x1,第二次初速度为v2,且v2=3v1,球落到斜面上前一瞬间的速度方向与斜面夹角为α2,落点与抛出点间的距离为x2,则
A. α2≠α1 B. α2=α1 C. x2=3x1 D. x2=9x1
【答案】BD
【解析】
画出物体落到斜面时的速度分解图,根据平抛运动水平位移和竖直位移的关系结合几何关系求解时间,然后表示出α以及水平位移x即可求解.
如图所示,由平抛运动的规律知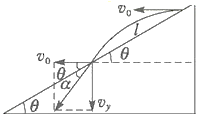
lsinθ=![]() gt2,lcosθ=v0t,解得:
gt2,lcosθ=v0t,解得:![]() ,由图知tan(α+θ)=
,由图知tan(α+θ)=![]() =2tanθ,所以α与抛出速度v0无关,故α1=α2,选项B正确,A错误;水平位移x=v0t=
=2tanθ,所以α与抛出速度v0无关,故α1=α2,选项B正确,A错误;水平位移x=v0t=![]() ;
;
∵v2=3v1,∴x2=9x1,故C错误,D正确;故选BD。

练习册系列答案
相关题目