题目内容
 如图所示,两根相同的轻弹簧S1、S2,劲度系数皆为k=4×102N/m.悬挂的重物的质量分别为
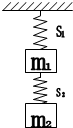
如图所示,两根相同的轻弹簧S1、S2,劲度系数皆为k=4×102N/m.悬挂的重物的质量分别为m1=2kg和m2=4kg.若不计弹簧质量,取g=10m/s2,则平衡时弹簧S1、S2的伸长量分别为( )
| A、10cm、15cm | B、15cm、10cm | C、10cm、5cm | D、5cm、10cm |
分析:以m2为研究对象可知,m2受弹簧拉力及本身的重力而处于平衡状态,故由平衡条件可求得弹簧S2的伸长量;
对整体进行受力分析,整体受重力、弹簧的拉力,由平衡条件可求得S1的伸长量.
对整体进行受力分析,整体受重力、弹簧的拉力,由平衡条件可求得S1的伸长量.
解答:解:m2受重力、弹簧的拉力而处于平衡状态,其拉力F2=kS2;
由共点力的平衡条件可知,kS2=m2g;
解得:S2=
=
=10cm;
同理对整体有:
kS1=(m1+m2)g
解得:
S1=
g=
=15cm;故B正确
故选:B.
由共点力的平衡条件可知,kS2=m2g;
解得:S2=
| m2g |
| k |
| 40 |
| 4×102 |
同理对整体有:
kS1=(m1+m2)g
解得:
S1=
| m1+m2 |
| k |
| 40+20 |
| 4×102 |
故选:B.
点评:本题中注意整体法的应用,整体法在高中物理中具有非常重要的作用,在解题中用好整体法可以化繁为简,提高解题速度.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
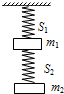 如图所示,两根相同的轻弹簧S1、S2,劲度系数皆为k=4×102N/m.悬挂的重物的质量分别为m1=2kg和m2=4kg.若不计弹簧质量,取g=10m/s2,则平衡时弹簧S1、S2的伸长量分别为( )
如图所示,两根相同的轻弹簧S1、S2,劲度系数皆为k=4×102N/m.悬挂的重物的质量分别为m1=2kg和m2=4kg.若不计弹簧质量,取g=10m/s2,则平衡时弹簧S1、S2的伸长量分别为( )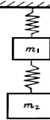 如图所示,两根相同的轻弹簧S1、S2,劲度系数皆为K=4×102N/m.悬挂的重物的质量分别为m1=2Kg、m2=4Kg.取g=10m/s2,则平衡时弹簧S1、S2的伸长量分别为( )
如图所示,两根相同的轻弹簧S1、S2,劲度系数皆为K=4×102N/m.悬挂的重物的质量分别为m1=2Kg、m2=4Kg.取g=10m/s2,则平衡时弹簧S1、S2的伸长量分别为( ) 如图所示,两根相同的橡皮绳OA、OB,开始夹角为0°,在O处打结吊一重50N的物体后,结点O刚好位于圆心.今将A、B分别沿圆周向两边移至A′、B′,使∠AOA′=∠BOB′=60°,欲使结点仍在圆心处,则此时结点处应挂物体的重量
如图所示,两根相同的橡皮绳OA、OB,开始夹角为0°,在O处打结吊一重50N的物体后,结点O刚好位于圆心.今将A、B分别沿圆周向两边移至A′、B′,使∠AOA′=∠BOB′=60°,欲使结点仍在圆心处,则此时结点处应挂物体的重量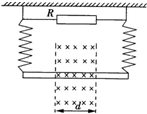 如图所示,两根相同的劲度系数为后的金属轻弹簧用两根等长的绝缘线悬挂在水平天花板上,弹簧的上端通过导线与阻值为R的电阻相连,弹簧的下端接一质量为m、长度为L、电阻为r的金属棒,金属棒始终处于宽度为d的垂直纸面向里磁感应强度为B的匀强磁场中.开始时弹簧处于原长,金属棒从静止释放,其下降高度为h时达到了最大速度.已知弹簧始终在弹性限度内,且当弹簧的形变量为x时,它的弹性势能为
如图所示,两根相同的劲度系数为后的金属轻弹簧用两根等长的绝缘线悬挂在水平天花板上,弹簧的上端通过导线与阻值为R的电阻相连,弹簧的下端接一质量为m、长度为L、电阻为r的金属棒,金属棒始终处于宽度为d的垂直纸面向里磁感应强度为B的匀强磁场中.开始时弹簧处于原长,金属棒从静止释放,其下降高度为h时达到了最大速度.已知弹簧始终在弹性限度内,且当弹簧的形变量为x时,它的弹性势能为