题目内容
9. 如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )
如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )| A. | 推力F的大小为2$\sqrt{3}$mg,弹簧的长度为l+$\frac{\sqrt{3}mg}{2k}$ | |
| B. | 若推力作用在A上,则F=2$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ | |
| C. | 作用在B上推力的最小值为$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ | |
| D. | 作用在A上推力的最小值为$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ |
分析 对于连接体问题,优先考虑以整体为研究对象,本题中以整体为研究对象,可以求出力F的大小,然后根据A处于平衡状态,可以求出弹簧弹力,从而进一步求出弹簧的原长.当推力沿斜面向上时取得最小值,由平衡条件求F的最小值.
解答  解:A、以整体为研究对象,受力分析有:
解:A、以整体为研究对象,受力分析有:
系统处于平衡状态,沿斜面方向有:Fcos60°=2mgsin60° ①
以A为研究对象沿斜面方向有重力沿斜面分析的分力等于弹簧的弹力:
kx=mgsin60° ②
x=l0-l ③
解①得:F=2$\sqrt{3}$mg
由②③得:l0=l+$\frac{\sqrt{3}mg}{2k}$.故A正确.
B、若推力作用在A上,由整体法可得:Fcos60°=2mgsin60°,则 F=2$\sqrt{3}$mg
以B为研究对象,则有kx=mgsin60°,x=$\frac{\sqrt{3}mg}{2k}$
此时弹簧的长度为 l′=l0+x=l+$\frac{\sqrt{3}mg}{k}$,故B正确.
C、当推力沿斜面向上时取得最小值,F的最小值为 Fmin=2mgsin60°=$\sqrt{3}$mg
此时弹簧的长度等于A项中弹簧的长度,为l+$\frac{\sqrt{3}mg}{2k}$.故C错误.
D、当推力沿斜面向上时取得最小值,F的最小值为 Fmin=2mgsin60°=$\sqrt{3}$mg
此时弹簧的长度等于B项中弹簧的长度,为l+$\frac{\sqrt{3}mg}{k}$.故D正确.
故选:ABD.
点评 对于连接体问题注意整体与隔离法的应用,正确选取研究对象然后受力分析,根据所处状态列方程求解.

练习册系列答案
相关题目
4.一枚火箭由地面竖直向上发射,其v-t图象如图所示.其中t3=3t 1,t2=2t1,v2=3v1,由图象可知( )


| A. | 火箭在t2-t3时间内向下运动 | |
| B. | 火箭能上升的最大高度为4v1 t1 | |
| C. | 火箭上升阶段的平均速度大小为$\frac{1}{2}$v2 | |
| D. | 火箭运动过程中的最大加速度大小为$\frac{{v}_{2}}{{t}_{3}}$ |
14.甲、乙两物体相距x,它们同时同向运动,乙在前面做初速度为0、加速度为a1的匀加速运动,甲在后面做初速度为v0、加速度为a2的匀加速运动,则( )
| A. | 若a1=a2,它们只能相遇一次 | B. | 若a1>a2,它们可能相遇两次 | ||
| C. | 若a1>a2,它们只能相遇一次 | D. | 若a1<a2,它们不能相遇 |
1. 如图所示,某同学在教室中站在体重计上研究超重与失重.她由稳定的站姿变化到稳定的蹲姿称为“下蹲”过程;由稳定的蹲姿变化到稳定的站姿称为“起立”过程.关于她的实验现象,下列说法中正确的是( )
如图所示,某同学在教室中站在体重计上研究超重与失重.她由稳定的站姿变化到稳定的蹲姿称为“下蹲”过程;由稳定的蹲姿变化到稳定的站姿称为“起立”过程.关于她的实验现象,下列说法中正确的是( )
 如图所示,某同学在教室中站在体重计上研究超重与失重.她由稳定的站姿变化到稳定的蹲姿称为“下蹲”过程;由稳定的蹲姿变化到稳定的站姿称为“起立”过程.关于她的实验现象,下列说法中正确的是( )
如图所示,某同学在教室中站在体重计上研究超重与失重.她由稳定的站姿变化到稳定的蹲姿称为“下蹲”过程;由稳定的蹲姿变化到稳定的站姿称为“起立”过程.关于她的实验现象,下列说法中正确的是( )| A. | 只有“起立”过程,才能出现失重的现象 | |
| B. | 只有“下蹲”过程,才能出现超重的现象 | |
| C. | “起立”、“下蹲”的过程,都能出现超重和失重的现象 | |
| D. | “起立”的过程,先出现超重现象后出现失重现象 |
18.通电导线在磁场中所受到的力叫( )
| A. | 洛伦兹力 | B. | 安培力 | C. | 电场力 | D. | 静电力 |
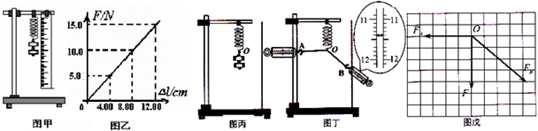
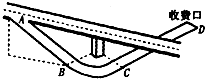 某高速公路的一个出口路段如图所示,情景简化:轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到D点停下.已知轿车在A点的速度vo=72km/h,AB长L1=150m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=36km/h,轮胎与BC段路面间的动摩擦因数u=0.5,最大静摩擦力可认为等于滑动摩擦力,C段长L2=50m,重力加速度g取10m/s2.
某高速公路的一个出口路段如图所示,情景简化:轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到D点停下.已知轿车在A点的速度vo=72km/h,AB长L1=150m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=36km/h,轮胎与BC段路面间的动摩擦因数u=0.5,最大静摩擦力可认为等于滑动摩擦力,C段长L2=50m,重力加速度g取10m/s2.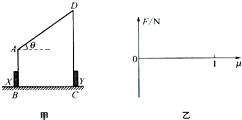 如图甲所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰好与两个固定在地面上的压力传感器X和Y相接触.图中AB高H=0.3m、AD长L=0.5m,斜面倾角θ=37°.可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数μ可以通过更换斜面表面的材料进行调节(调节范围是0≤μ≤1).sin37°=0.6,cos37°=0.8,重力加速度取g=10m/s2.
如图甲所示,质量足够大、截面是直角梯形的物块静置在光滑水平地面上,其两个侧面恰好与两个固定在地面上的压力传感器X和Y相接触.图中AB高H=0.3m、AD长L=0.5m,斜面倾角θ=37°.可视为质点的小物块P(图中未画出)质量m=1kg,它与斜面的动摩擦因数μ可以通过更换斜面表面的材料进行调节(调节范围是0≤μ≤1).sin37°=0.6,cos37°=0.8,重力加速度取g=10m/s2.