题目内容
19.(1)小明利用如图甲所示的装置,探究弹簧弹力F与伸长量△l的关系,由实验绘出F与△l的关系图线如图乙所示,该弹簧劲度系数为125N/m.(2)小丽用如图丙所示的装置验证“力的平行四边形定则”.用一木板竖直放在铁架台和弹簧所在平面后.其部分实验操作如下,请完成下列相关内容:
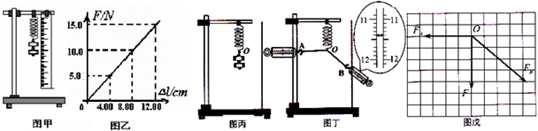
a.如图丙,在木板上记下悬挂两个钩码时弹簧末端的位置O;
b.卸下钩码然后将两绳套系在弹簧下端,用两弹簧称将弹簧末端拉到同一位置O,记录细绳套AO、BO的方向及两弹簧称相应的读数.图丁中B弹簧称的读数为11.40N;
c.小丽在坐标纸上画出两弹簧拉力FA、FB的大小和方向如图丁所示,请你用作图工具在答题卷上相应位置作出FA、FB的合力F′,并求出合力的理论值为7.98N;
d.已知钩码的重力,可得弹簧所受的拉力F如图戊所示,
e.最后观察比较F和F′,得出结论.
分析 (1)根据胡克定律知,图线的斜率表示劲度系数,结合斜率求出劲度系数的大小.
(2)在“力的平行四边形定则”实验中.需要测量力的大小和方向,弹簧秤读数时,搞清每一格的分度为多少.
根据平行四边形定则作出合力;并由图象得出对应的合力大小
解答 解:(1)图线的斜率表示劲度系数:$k=\frac{15}{0.12}=125N/m$.
(2)实验时,需记录细绳套AO、BO的方向以及两弹簧称相应的读数.弹簧秤的最小分度为0.1N,故图丁中B弹簧称的读数为11.40N.
根据平行四边形定则作出合力,如图所示.由图利用几何关系可知,合力的理论值约为7.98N;
故答案为:①125;②方向,11.40,如图所示;7.98
;
点评 本题考查了求弹簧的劲度系数和验证平行四边形定则,知道F-△l图象斜率的物理意义,以及知道验证平行四边形定则实验的原理,掌握弹簧秤的读数方法.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
10.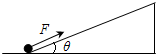 如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动,若斜面足够长,表面光滑,倾角为θ.经时间t,恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动,若斜面足够长,表面光滑,倾角为θ.经时间t,恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
 如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动,若斜面足够长,表面光滑,倾角为θ.经时间t,恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )
如图所示,一质量为m的物体在沿斜面向上的恒力F作用下,由静止从底端向上做匀加速直线运动,若斜面足够长,表面光滑,倾角为θ.经时间t,恒力F做功80J,此后撤去恒力F,物体又经时间t回到出发点,且回到出发点时的速度大小为v,若以地面为重力势能的零势能面,则下列说法中正确的是( )| A. | 物体回到出发点时的机械能小于80J | |
| B. | 在撤去力F前的瞬间,力F的功率大小是$\frac{2}{3}$mgvsinθ | |
| C. | 撤去力F前的运动过程中,物体的重力势能一直在增加,撤去力F后的运动过程中物体的重力势能一直在减少 | |
| D. | 撤去力F前的运动过程中,物体的动能一直在增加,撤去力F后的运动过程中物体的动能一直在减少 |
7.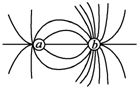 法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )
法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )
 法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )
法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )| A. | a、b为异种电荷,a的电荷量大于b的电荷量 | |
| B. | a、b为异种电荷,a的电荷量小于b的电荷量 | |
| C. | a、b为同种电荷,a的电荷量大于b的电荷量 | |
| D. | a、b为异种电荷,a的电荷量等于b的电荷量 |
4.有一种测定重力加速度g的方法,叫“对称自由下落法”,它可将测定g归结于测定长度和时间.实验中所用稳定的氦氖激光的波长为长度标准,利用光学干涉的方法测距离,以铷原子钟测时间,因此能将g值测得很准,具体做法是:将真空长直管沿竖直方向放置,测得自某点O竖直向上抛出小球到小球落回O点的时间间隔为T2,在上述小球的运动过程中,还测得小球两次经过比O点高H的P点的时间间隔为T1,则用T1、T2和H表示g为( )
| A. | $\frac{8H}{T_2^2-T_1^2}$ | B. | $\frac{4H}{{{T}_{2}}^{2}-{{T}_{1}}^{2}}$ | C. | $\frac{8H}{({T}_{2}-{T}_{1})^{2}}$ | D. | $\frac{H}{4({T}_{2}-{T}_{1})^{2}}$ |
11.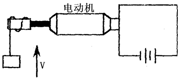 如图为直流电动机提升重物的装置,重物G=500N,电源电动势E=110V,不计电源内阻及各处摩擦,当电动机以ν=0.90m/s的恒定速度向上提升重物时,电路中的电流I=5.0A,可以判断( )
如图为直流电动机提升重物的装置,重物G=500N,电源电动势E=110V,不计电源内阻及各处摩擦,当电动机以ν=0.90m/s的恒定速度向上提升重物时,电路中的电流I=5.0A,可以判断( )
 如图为直流电动机提升重物的装置,重物G=500N,电源电动势E=110V,不计电源内阻及各处摩擦,当电动机以ν=0.90m/s的恒定速度向上提升重物时,电路中的电流I=5.0A,可以判断( )
如图为直流电动机提升重物的装置,重物G=500N,电源电动势E=110V,不计电源内阻及各处摩擦,当电动机以ν=0.90m/s的恒定速度向上提升重物时,电路中的电流I=5.0A,可以判断( )| A. | 电源的总功率为550WA.电动机消耗的总功率为550W | |
| B. | 提升重物消耗的功率为450W | |
| C. | 电动机线圈的电阻为22Ω | |
| D. | 电动机线圈的电阻为4Ω |
8.如图是某物体做直线运动的vt图象,由图象可得到的正确结果是( )
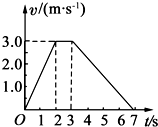

| A. | t=1s时物体的加速度大小为1.0m/s2 | |
| B. | t=5s时物体的加速度大小为0.75m/s2 | |
| C. | 第3s内物体的位移为1.5m | |
| D. | 物体在加速过程的速度变化率比减速过程的速度变化率大 |
9. 如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )
如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )
 如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )
如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )| A. | 推力F的大小为2$\sqrt{3}$mg,弹簧的长度为l+$\frac{\sqrt{3}mg}{2k}$ | |
| B. | 若推力作用在A上,则F=2$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ | |
| C. | 作用在B上推力的最小值为$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ | |
| D. | 作用在A上推力的最小值为$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ |