题目内容
17.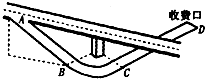 某高速公路的一个出口路段如图所示,情景简化:轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到D点停下.已知轿车在A点的速度vo=72km/h,AB长L1=150m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=36km/h,轮胎与BC段路面间的动摩擦因数u=0.5,最大静摩擦力可认为等于滑动摩擦力,C段长L2=50m,重力加速度g取10m/s2.
某高速公路的一个出口路段如图所示,情景简化:轿车从出口A进入匝道,先匀减速直线通过下坡路段至B点(通过B点前后速率不变),再匀速率通过水平圆弧路段至C点,最后从C点沿平直路段匀减速到D点停下.已知轿车在A点的速度vo=72km/h,AB长L1=150m;BC为四分之一水平圆弧段,限速(允许通过的最大速度)v=36km/h,轮胎与BC段路面间的动摩擦因数u=0.5,最大静摩擦力可认为等于滑动摩擦力,C段长L2=50m,重力加速度g取10m/s2.(1)若轿车到达B点时速度为v1=18km/h,求轿车在AB段加速度的大小;
(2)为保证行车安全,车轮不侧滑,求水平圆弧段BC半径R的最小值;
(3)轿车从A点到D点所用的最短时间为多少?
分析 (1)轿车在AB段做匀减速直线运动,已知初速度、位移和末速度,根据速度位移关系公式求解加速度.
(2)轿车在BC段做匀速圆周运动,由静摩擦力充当向心力,为保证行车安全,车轮不打滑,所需要的向心力不大于最大静摩擦力,据此列式求解半径R的最小值.
(3)分三段,分别由运动学公式求解时间,即可得到所用的最短总时间.
解答 解:(1)v0=72km/h=20m/s,v1=18km/h=5m/s,
根据速度位移公式得,${{v}_{0}}^{2}-{{v}_{1}}^{2}=2a{L}_{1}$,解得轿车在AB段的加速度大小$a=\frac{400-25}{300}m/{s}^{2}=1.25m/{s}^{2}$.
(2)汽车在BC段做圆周运动,静摩擦力提供 向心力,
${F}_{1}=m\frac{{v}^{2}}{R}$,
为了确保安全,则须满足F1≤μmg,
代入数据解得R≥20m,即Rmin=20m.
(3)设AB段时间为t1,BC段时间为t2,CD段时间为t3,全程的最短时间为t,
${L}_{1}=\frac{{v}_{0}+v}{2}{t}_{1}$,
$\frac{1}{2}πR=v{t}_{2}$,
${L}_{2}=\frac{v}{2}{t}_{3}$,
总时间t=t1+t2+t3,
代入数据解得t=23.14s.
答:(1)轿车在AB段加速度的大小为1.25m/s2;
(2)水平圆弧段BC半径R的最小值为20m;
(3)轿车从A点到D点所用的最短时间为23.14s.
点评 本题是运动学与动力学综合题,能结合物体的运动情况,灵活选择运动学的公式形式是关键,当不涉及加速度而要求时间时,可用位移等于平均速度乘以时间来求.

练习册系列答案
相关题目
7.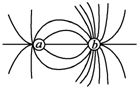 法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )
法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )
 法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )
法拉第首先提出用电场线形象生动地描绘电场,如图所示,为点电荷a、b所形成电场的电场线分布,以下几种说法正确的是( )| A. | a、b为异种电荷,a的电荷量大于b的电荷量 | |
| B. | a、b为异种电荷,a的电荷量小于b的电荷量 | |
| C. | a、b为同种电荷,a的电荷量大于b的电荷量 | |
| D. | a、b为异种电荷,a的电荷量等于b的电荷量 |
8.如图是某物体做直线运动的vt图象,由图象可得到的正确结果是( )
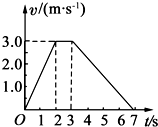

| A. | t=1s时物体的加速度大小为1.0m/s2 | |
| B. | t=5s时物体的加速度大小为0.75m/s2 | |
| C. | 第3s内物体的位移为1.5m | |
| D. | 物体在加速过程的速度变化率比减速过程的速度变化率大 |
5. 如图所示,真空中A、B两点固定两个等量正电荷,一个具有初速度的带负电的粒子仅在这两个电荷作用下可能做( )
如图所示,真空中A、B两点固定两个等量正电荷,一个具有初速度的带负电的粒子仅在这两个电荷作用下可能做( )
 如图所示,真空中A、B两点固定两个等量正电荷,一个具有初速度的带负电的粒子仅在这两个电荷作用下可能做( )
如图所示,真空中A、B两点固定两个等量正电荷,一个具有初速度的带负电的粒子仅在这两个电荷作用下可能做( )| A. | 匀速直线运动 | B. | 变速直线运动 | C. | 匀变速曲线运动 | D. | 匀速圆周运动 |
12.“神舟十号”飞船发射后与“天官一号”进行交会对接,三位航天员人住“天宫”完成一系列实验,“神舟十号”与“天官一号”对接后做匀速圆周运动,运行周期为90分钟.对接后“天官一号”的( )
| A. | 运行速度大于第一宇宙速度 | |
| B. | 航天员可以用天平测出物体的质量 | |
| C. | 角速度为地球同步卫星角速度的16倍 | |
| D. | 加速度大于赤道上静止物体随地球自转的加速度 |
2.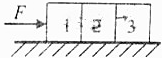 三个质量相同的物体紧靠在一起放在光滑水平桌面上,如图所示,如果1物体受到一个水平推力F的作用,则1物体对2物体用力为( )
三个质量相同的物体紧靠在一起放在光滑水平桌面上,如图所示,如果1物体受到一个水平推力F的作用,则1物体对2物体用力为( )
 三个质量相同的物体紧靠在一起放在光滑水平桌面上,如图所示,如果1物体受到一个水平推力F的作用,则1物体对2物体用力为( )
三个质量相同的物体紧靠在一起放在光滑水平桌面上,如图所示,如果1物体受到一个水平推力F的作用,则1物体对2物体用力为( )| A. | F | B. | $\frac{F}{2}$ | C. | $\frac{F}{3}$ | D. | $\frac{2F}{3}$ |
9. 如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )
如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )
 如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )
如图所示,水平固定倾角为60°的光滑斜面上有两个质量均为m的小球A、B,它们用劲度系数为k的轻质弹簧连接,现对B施加一水平向右的推力F使A、B均静止在斜面上,此时弹簧的长度为l,则下列说法正确的是( )| A. | 推力F的大小为2$\sqrt{3}$mg,弹簧的长度为l+$\frac{\sqrt{3}mg}{2k}$ | |
| B. | 若推力作用在A上,则F=2$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ | |
| C. | 作用在B上推力的最小值为$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ | |
| D. | 作用在A上推力的最小值为$\sqrt{3}$mg,此时弹簧的长度为l+$\frac{\sqrt{3}mg}{k}$ |
7.下列关于磁感线的说法中正确的是( )
| A. | 磁感线是磁场中真实存在的曲线 | |
| B. | 沿着磁感线的方向,磁场越来越弱 | |
| C. | 磁感线可以相交,相交处表示磁场互相叠加 | |
| D. | 所有的磁感线都是封闭的 |
 如图所示,高h=0.80m的光滑弧形轨道与水平光滑轨道相切且平滑连接.将一个质量m=0.40kg的物块(可视为质点)从弧形轨道顶端由静止释放,物块滑至水平轨道后,从水平轨道右侧边缘O点水平飞出,落到水平地面的P点,P点距O点的水平距离x=1.6m.不计一切摩擦和空气阻力,取重力加速度g=10m/s2.求:
如图所示,高h=0.80m的光滑弧形轨道与水平光滑轨道相切且平滑连接.将一个质量m=0.40kg的物块(可视为质点)从弧形轨道顶端由静止释放,物块滑至水平轨道后,从水平轨道右侧边缘O点水平飞出,落到水平地面的P点,P点距O点的水平距离x=1.6m.不计一切摩擦和空气阻力,取重力加速度g=10m/s2.求: