Question

【题目】如图所示，一水平的浅色传送带长32m，传送带上左端放置一煤块（可视为质点）。初始时，传送带与煤块都是静止的，煤块与传送之间的动摩擦因数为0.2，从某时刻起，传送带以4m/s2的加速度沿顺时针方向加速运动，经一定时间t后，马上以同样大小的加速度做匀减速运动直到停止。最后，煤块恰好停在传送带的右端，此过程中煤块在传送带上留下了一段黑色痕迹（g=10m/s2）。求：

(1)传送带的加速时间t；

(2)当煤块停止运动时，煤块在传送带上留下黑色痕迹的长度。

Answer 1

【答案】(1)3s；(2)16m

【解析】

(1)煤块能受到的最大静摩擦力fm=μmg，对应最大加速度

am=μg=2m/s2＜a=4m/s2

所以两物体的运动情景可由图表示

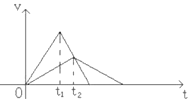
研究煤块运动的全过程

解得

t2=4s

则

v1=amt2=8m/s

研究皮带的运动0－t1时间内，v=at1，t1－t2时间内

v1=v－a(t2－t1)

可知

t=t1=3s，v=12m/s

(2)0－t2时间内，煤块相对于皮带向左滑，皮带向右内前进的距离

煤块向右前进的距离

s1=v1t2=12m

黑色痕迹长

ΔL1=s－s1=16m

t1－t2，煤块相对于皮带向右滑行，相对距离

则

ΔL1>ΔL2

所以

s=ΔL1=16m