题目内容
【题目】如图所示，水平传送带以一定速度匀速运动，将质量m=1kg的小物块轻轻放在传送带上的P点，物块运动到A点后被水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑。B、C为圆弧上的两点，其连线水平，已知圆弧对应圆心角
，A点距水平面的高度h=3.2m，圆弧C点与斜面CD恰好相切，小物块到达C点时的速度大小与B点相等，并沿固定斜面向上滑动，小物块从C点到第二次经过D点的时间间隔为1.6s，已知小物块与斜面间的动摩擦因数
，重力加速度g取10m/s2，取
，
，求：
(1)小物块从A到B的运动时间；
(2)小物块离开A点时的水平速度大小；
(3)斜面上C、D点间的距离。
【答案】(1)0.8s；(2)6m/s；(3)3.92m
【解析】
(1)小物块从A到B做平抛运动
解得
(2)到达B点时的竖直速度
由题可知
解得
(3)滑块到达C点时的速度与B点速度相等
斜面CD的倾角为
，滑块上滑过程中，根据牛顿第二定律
解得加速度
上滑的时间
上滑的距离
下滑过程中，根据牛顿第二定律
解得加速度
下滑的位移
因此CD间距离
【题目】某同学利用如图甲所示的电路研究小灯泡的伏安特性曲线。
可使用的器材有：
小灯泡L（额定电压6.8 V，额定功率3.6 W）；
滑动变阻器R（最大阻值10 ）；
电压表V（量程0~9 V，内阻约9 k）；
电流表A（量程0~0.6 A，内阻约0.6 ）；
电源E（电动势8 V，内阻1.0 Ω）；
开关S；导线若干。
（1）按原理图甲将图乙中的实物连线补充完整_____。
（2）连接好电路，将滑动变阻器滑片移至最左端，闭合开关后，移动滑片，进行实验，测出如下表所示的数据，并根据这些实验数据在丙图坐标上进行描点，其中有一个点尚未描上，请你描上该点，并作出I-U图线_____。
I/A | 0 | 0.20 | 0.30 | 0.36 | 0.42 | 0.46 | 0.48 | 0.50 |
U/V | 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
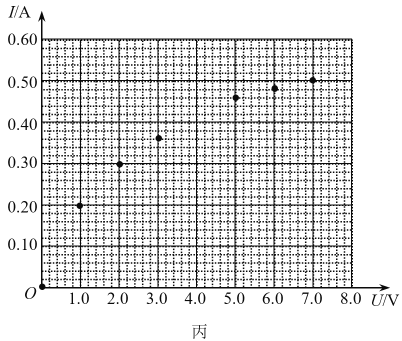
（3）将该灯泡与阻值为4 Ω定值电阻串联后，接在电动势为8.0 V、内阻为1.0 Ω的电源两端，若将定值电阻与电源等效为新的电源，则新电源的电动势为8.0 V、内阻为_____Ω ，短路电流为__________A，此时灯泡的功率约为____________W（结果保留两位有效数字）。
