Question

【题目】为了研究过山车的原理，物理兴趣小组提出了下列设想：如图所示，取一个与水平方向夹角θ＝30°，长L＝0.8 m的倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道都是光滑的．其中AB与BC轨道以微小圆弧相接，竖直圆轨道的半径R＝0.6 m．现使一个质量m＝0.1 kg的小物块从A点开始以初速度v0沿倾斜轨道滑下，g取10 m/s2．问：

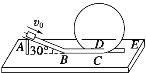
(1)若v0＝5.0 m/s，则小物块到达B点时的速度为多大？

(2)若v0＝5.0 m/s，小物块到达竖直圆轨道的最高点时对轨道的压力为多大？

(3)为了使小物块在竖直圆轨道上运动时能够不脱离轨道，v0大小应满足什么条件？

Answer 1

【答案】(1) (2) 0.5N (3) v0≤2m/s 或v0≥

【解析】

(1)对小物块从A点到B点利用动能定理

得

(2)对小物块从B点到圆轨道最高点利用动能定理

得：v=3m/s

在圆轨道最高点，由牛顿第二定律

得：FN=0. 5N

由牛顿第三定律可知：FN′＝FN＝0.5N。

(3)情形一：物体能完成圆运动

在最高点：由，得，

对小物块从A点到圆轨道最高点利用动能定理

解得：

情形二：物体运动到圆轨道圆心等高处速度为零

对小物块从A点到圆轨道圆心等高处利用动能定理

解得：v0=2m/s

综合以上两种情形可得：v0≤2m/s 或v0≥