��Ŀ����
14��̽�¹������ڷ�����������2014��10��24��2ʱ���й��������Ƿ������ķ������գ����ս������������Ϊh��Բ�ι��������������뾶ΪR���������������ٶ�Ϊg��������������ΪG��������˵����ȷ���ǣ�������| A�� | �����������ڹ�������ϵļ��ٶ�Ϊ��$\frac{R}{R+h}$��2g | |
| B�� | �������������������е�����Ϊ2��$\sqrt{\frac{R}{g}}$ | |
| C�� | �����������ڹ�������ϵ������ٶ�Ϊ$\sqrt{g��R+h��}$ | |
| D�� | �����ƽ���ܶ�Ϊ$\frac{3g}{4��GR}$ |
���� �����������������������������г���ʽ������ţ�ٵڶ����ɵó������������ڹ�������ϵļ��ٶȣ�
��������������ʱ���������ṩԲ���˶��������г���ʽ��⣻
�������������ṩ���������Ƶ������ٶ���⣻
�����ܶȶ�����⣮
��� �⣺A�����������������������������ȵ�
mg=$\frac{GMm}{{R}^{2}}$
����ţ�ٵڶ����ɵ�
�����������ڹ�������ϵļ��ٶ�a=$\frac{GM}{{r}^{2}}$=��$\frac{R}{R+h}$��2g����A��ȷ��
B����������������ʱ���������ṩԲ���˶��������У�
$\frac{GMm}{{r}^{2}}$=m$\frac{{4��}^{2}}{{T}^{2}}$r���ɵ�T=2��$\sqrt{\frac{{r}^{3}}{GM}}$=2��$\sqrt{\frac{{��R+h��}^{3}}{{gR}^{2}}}$����B����
C����������������ϵ������ٶ�����$\frac{GMm}{{��R+h��}^{2}}$=m$\frac{{v}^{2}}{R+h}$
��v=$\sqrt{\frac{GM}{R+h}}$=$\sqrt{\frac{{gR}^{2}}{R+h}}$����C����
D��������ܶ� ��=$\frac{M}{\frac{4{��R}^{3}}{3}}$=$\frac{3g}{4��GR}$����D��ȷ��
��ѡ��AD��
���� ���������ṩԲ���˶����������������������������������ǽ�������������Ҫ���ֵ㣬�ؼ���������ع�ʽ����ʽ�任��

 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�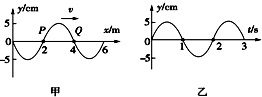
| A�� | ���в��IJ���Ϊ��=2m | |
| B�� | ��ͼ������ͼ�����ʵ�Q����ͼ�� | |
| C�� | ���в��Ĵ����ٶ�Ϊv=3m/s | |
| D�� | ���в��IJ�Դ������Ϊ���� |
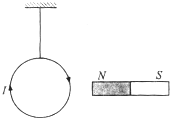 19���Ͱ���ͨ���Ƚϻ��ε����Ĵų������ų��������ԣ�����˷��ӵ������ۣ�˵���˴���Ĵų��͵����Ĵų�������ͬ����Դ����������ĵ籾�ʣ�����ͨ�����������Է���˵��������ͼ��ʾ���������廷�����ڴ��帽�������廷�����ߵ�ƫת����ǣ�������
19���Ͱ���ͨ���Ƚϻ��ε����Ĵų������ų��������ԣ�����˷��ӵ������ۣ�˵���˴���Ĵų��͵����Ĵų�������ͬ����Դ����������ĵ籾�ʣ�����ͨ�����������Է���˵��������ͼ��ʾ���������廷�����ڴ��帽�������廷�����ߵ�ƫת����ǣ�������| A�� | �������¿������廷˳ʱ����ת��ͬʱ��������ƫת | |
| B�� | �������¿������廷��ʱ����ת��ͬʱ��������ƫת | |
| C�� | ���廷����ת����������ƫת | |
| D�� | ���廷����ת����������ƫת |
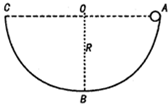 ��ͼ��ʾ����ֱƽ������һ�⻬��Ե��Բ��������ڷ���ˮƽ������ƽ��ƽ�е���ǿ�糡�У�������˵�A��C�߶���ͬ����Բ��O��ͬһˮƽ���ϣ�����İ뾶ΪR0��һ������Ϊm�Ĵ������С��Ӳ��Ҷ˵�A�����ٵ��ع���»���������͵�Bʱ�Բ۵�ѹ��Ϊ2mg������С��Ļ��������У��У�������
��ͼ��ʾ����ֱƽ������һ�⻬��Ե��Բ��������ڷ���ˮƽ������ƽ��ƽ�е���ǿ�糡�У�������˵�A��C�߶���ͬ����Բ��O��ͬһˮƽ���ϣ�����İ뾶ΪR0��һ������Ϊm�Ĵ������С��Ӳ��Ҷ˵�A�����ٵ��ع���»���������͵�Bʱ�Բ۵�ѹ��Ϊ2mg������С��Ļ��������У��У�������| A�� | С��B��ʱ���ٶȴ�СΪ$\sqrt{2gR}$ | |
| B�� | С��B��ʱ���ٶȴ�СΪ$\sqrt{gR}$ | |
| C�� | С���ڻ��������е�����ٶ�Ϊ$\sqrt{��\sqrt{5}-1��gR}$ | |
| D�� | С���ڻ��������е�����ٶ�Ϊ$\sqrt{2gR}$ |
 ��ͼ��ʾ���̶���Բ�������ˮƽ��ƽ�����ӣ������ˮƽ����⻬������Ϊm�����B�����ʵ���˨�Ӿ�ֹ��ˮƽ���ϣ������Ҷ˹̶�������Ϊ3m�����A��Բ������Ͼ���ˮƽ���h���ɾ�ֹ�ͷţ���B��ײ������Bһ���˶�����B��ճ������
��ͼ��ʾ���̶���Բ�������ˮƽ��ƽ�����ӣ������ˮƽ����⻬������Ϊm�����B�����ʵ���˨�Ӿ�ֹ��ˮƽ���ϣ������Ҷ˹̶�������Ϊ3m�����A��Բ������Ͼ���ˮƽ���h���ɾ�ֹ�ͷţ���B��ײ������Bһ���˶�����B��ճ������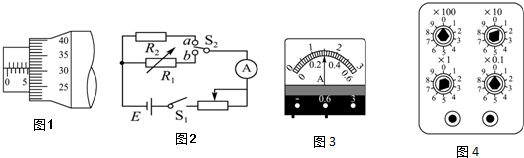
 ��ͼ��ʾ�������Ϊ��=30���б���ϣ����������⻬���㹻���ĵ���ac��bd���������ľ���Ϊl=0.1m��������ĵ�a��b����е���R=0.06�������������ϴ�ֱ�ڵ������һ������Ϊm=5��10-3kg������Ϊr=0.02��������ΪL=0.12m�Ľ�����cd������װ��������OO������沿�֣����ڴ�ֱ��б�����ǿ�ų��У��ֽ�������cd�ɾ�ֹ�ͷţ����»�x=10m�պþ�������OO�����ų���ʱ��������cd�Ϳ�ʼ�����»���ͨ������R�еĸ�Ӧ�����ķ����Ǵ�a��b�����Ƶ����ĵ�������ܵ�Ħ�����������ٶ�Ϊg=10m/s2����
��ͼ��ʾ�������Ϊ��=30���б���ϣ����������⻬���㹻���ĵ���ac��bd���������ľ���Ϊl=0.1m��������ĵ�a��b����е���R=0.06�������������ϴ�ֱ�ڵ������һ������Ϊm=5��10-3kg������Ϊr=0.02��������ΪL=0.12m�Ľ�����cd������װ��������OO������沿�֣����ڴ�ֱ��б�����ǿ�ų��У��ֽ�������cd�ɾ�ֹ�ͷţ����»�x=10m�պþ�������OO�����ų���ʱ��������cd�Ϳ�ʼ�����»���ͨ������R�еĸ�Ӧ�����ķ����Ǵ�a��b�����Ƶ����ĵ�������ܵ�Ħ�����������ٶ�Ϊg=10m/s2����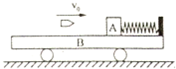 ��ͼ��ʾ������M=9kgС��B��ֹ�ڹ⻬ˮƽ���ϣ�С���Ҷ˹̶�һ���ʵ��ɣ�����m=0.9kg��ľ��A������Ϊ�ʵ㣩�������ɷ��ò����ھ�ֹ״̬��A�뵯�ɲ�˨�ӣ����ɴ���ԭ��״̬��ľ��A�Ҳ�ϱ���⻬��ľ��A������ֲڣ���Ħ��������=0.75��һ������m0=0.1kg���ӵ���v0=100m/s���ٶ�ˮƽ���ҷ�����˲�����ľ�鲢�������У�������ľ��A�պò���С����˵�������
��ͼ��ʾ������M=9kgС��B��ֹ�ڹ⻬ˮƽ���ϣ�С���Ҷ˹̶�һ���ʵ��ɣ�����m=0.9kg��ľ��A������Ϊ�ʵ㣩�������ɷ��ò����ھ�ֹ״̬��A�뵯�ɲ�˨�ӣ����ɴ���ԭ��״̬��ľ��A�Ҳ�ϱ���⻬��ľ��A������ֲڣ���Ħ��������=0.75��һ������m0=0.1kg���ӵ���v0=100m/s���ٶ�ˮƽ���ҷ�����˲�����ľ�鲢�������У�������ľ��A�պò���С����˵�������