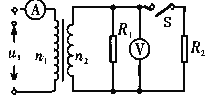
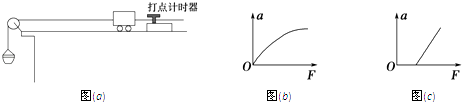
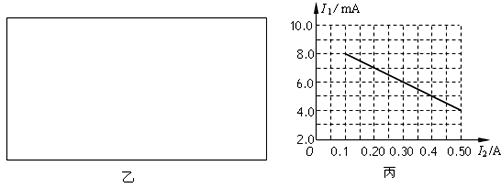
��Ŀ����
����Ŀ����ͼ��ʾ���⻬б��AB��ֲ�б��BC�Խӣ�һ����m=1.0kg��С�����A���ɾ�ֹ���£���֪AB��б�����Ϊ53�㣬A����B������ˮƽ��ĸ߶�h=0.8m����б��Խӵ�B����һ�κ�С��Բ���Ա�֤С�������ʱ����ײ�����Ե���B��ʱͬ����С���ٶȳ���BCб�棬��֪BC��б�����Ϊ37�㣬������б��BC��Ķ�Ħ��������=0.5���������˶�������ʼ��δ����б�棬�ӻ��鵽��B��ʱ�𣬾�0.6s ����ͨ��C�㣮��gȡ10m/s2 �� sin37��=0.6��cos37��=0.8����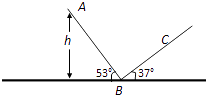
��1��С���鵽��B��ʱ�ٶȵĴ�С��
��2��С������BCб�������˶�ʱ���ٶȵĴ�С��
��3��BC֮��ľ��룮
���𰸡�
��1���⣺��A��B���ݶ��ܶ������У�
![]()
��ã� ![]()
��С���鵽��B��ʱ�ٶȵĴ�С4m/s��
��2���⣺С������BCб�������˶�ʱ������ţ�ٵڶ����ɣ��У�
mgsin37��+��mgcos37��=ma1
��ã�a1=gsin37��+��gcos37��=10��0.6+0.5��10��0.8=10 ![]()
��С������BCб�������˶�ʱ���ٶȵĴ�С ![]() ��
��
��3���⣺С�����B�������ȼ��ٵ��ٶ�Ϊ0��ʱ��
![]()
�ٶȼ�Ϊ0���������ȼ���ֱ���˶�������ţ�ٵڶ����ɣ���
![]()
��� ![]()
�����˶���λ�ƣ� ![]()
�����ȼ����˶���λ�ƣ� ![]()
BC֮��ľ��� ![]()
�� BC֮��ľ���0.76m��
����������1���ȸ��ݶ��ܶ�������������͵�ʱ���ٶȣ�2���Ի��������������ֱ�������ϻ��к����»��еļ��ٶȣ���3�������˶�ѧ��ʽ����BC��ľ��룮
�����㾫����������Ҫ�������ȱ���ֱ���˶����ٶȡ�λ�ơ�ʱ��Ĺ�ϵ�Ͷ��ܶ������ۺ�Ӧ�õ����֪ʶ�㣬��Ҫ�����ٶȹ�ʽ��V=V0+at��λ�ƹ�ʽ��s=v0t+1/2at2���ٶ�λ�ƹ�ʽ��vt2-v02=2as�����ϸ�ʽ��Ϊʸ��ʽ��Ӧ��ʱӦ�涨������Ȼ���ʸ����Ϊ��������⣬ͨ��ѡ���ٶȷ���Ϊ�������Ǹ�������һ�µ�ȡ��+��ֵ�����������෴��ȡ��-��ֵ��Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݲ�����ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�