题目内容
4. 如图所示,水平放置的传送带以速度v=2m/s向右运行,现将一小物体轻轻地放在传送带A端,物体与传送带间的动摩擦因数μ=0.2,若A端与B端相距4m,求(g取10m/s2)
如图所示,水平放置的传送带以速度v=2m/s向右运行,现将一小物体轻轻地放在传送带A端,物体与传送带间的动摩擦因数μ=0.2,若A端与B端相距4m,求(g取10m/s2)(1)物体由A端到B端的时间和物体到B端时的速度;
(2)物体从A处传送到B处的最短时间和传送带对应的最小运行速率.
分析 (1)物体在摩擦力的作用下加速运动,先根据牛顿第二定律求解出加速度,然后假设一直加速,根据运动学公式求出加速的位移,再判断物体有没有到达B端,发现没有到达B端,接下来物体做匀速运动直到B端,分匀加速和匀速两个过程,分别求出这两个过程的时间即可;
(2)从A至B的时间最短,由运动规律可知,当物体从A至B一直做匀加速运动时,所需时间最短.
解答 解:(1)设运动过程中物体的加速度为a,根据牛顿第二定律得:μmg=ma
求得:a=2m/s2
设达到皮带速度v时发生的位移为s1,所用时间为t1,则有:
v2=2as1
解得:s1=1m
根据速度公式有:v=at1
解得时间为:t1=1s
此时距离B端为:s2=4m-s1=4-1=3m
接下来做匀速运动的时间为:t2=$\frac{{s}_{2}}{v}$═1.5s
所以有:t=t1+t2=2.5s
物体最后阶段是匀速,故末速度为2m/s,
(2)物体从A匀加速运动到B时,传送时间最短,则:L=$\frac{1}{2}$at2
得行李运动的最短时间为:${t}_{min}=\sqrt{\frac{2L}{a}}=\sqrt{\frac{2×4}{2}}=2s$,
此时传送带对应的运行速率为v′,v′≥atmin=4m/s;
故传送带对应的最小运行速率为4m/s.
答:(1)物体由A端到B端的时间为2.5s,物体到B端时的速度为2m/s;
(2)物体从A处传送到B处的最短时间为2s,传送带对应的最小运行速率为4m/s.
点评 本题关键要对滑块受力分析后,根据牛顿第二定律求解出加速度,再结合运动学公式列式求解.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
16.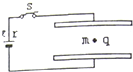 平行板电容器两板间有匀强电场,其中有一个带电液滴处于静止,如图所示.当发生下列哪些变化时,液滴将向上运动( )
平行板电容器两板间有匀强电场,其中有一个带电液滴处于静止,如图所示.当发生下列哪些变化时,液滴将向上运动( )
 平行板电容器两板间有匀强电场,其中有一个带电液滴处于静止,如图所示.当发生下列哪些变化时,液滴将向上运动( )
平行板电容器两板间有匀强电场,其中有一个带电液滴处于静止,如图所示.当发生下列哪些变化时,液滴将向上运动( )| A. | 将电容器的下极板稍稍下移 | B. | 将电容器的上极板稍稍下移 | ||
| C. | 紧贴上级板插入一块薄金属板 | D. | 上极板向左移一些 |
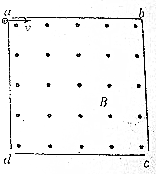 边长为L的正方形区域内分布着磁感应强度为B的匀强磁场,磁场方向垂直纸面向外,一电荷量为q、质量为m的带正电粒子以速度v(未知)从α处沿ab边方向进入磁场,试求:
边长为L的正方形区域内分布着磁感应强度为B的匀强磁场,磁场方向垂直纸面向外,一电荷量为q、质量为m的带正电粒子以速度v(未知)从α处沿ab边方向进入磁场,试求: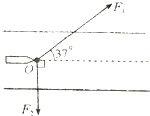 如图所示,有艘小船由两位纤夫拉着沿河道(图中虚线方向)往上游航行,已知其中一纤夫拉力的大小为F1=1000N,方向与河道成37°,另一纤夫拉力F2方向与河道垂直,求:
如图所示,有艘小船由两位纤夫拉着沿河道(图中虚线方向)往上游航行,已知其中一纤夫拉力的大小为F1=1000N,方向与河道成37°,另一纤夫拉力F2方向与河道垂直,求: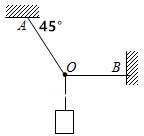 三段不可伸长的细绳OA、OB、OC共同悬挂一重物,如图所示,若重物的质量为100N,问OA、OB细绳的拉力分别为多大?
三段不可伸长的细绳OA、OB、OC共同悬挂一重物,如图所示,若重物的质量为100N,问OA、OB细绳的拉力分别为多大?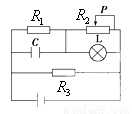
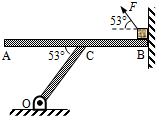 如图所示,质量M=1.6kg的均匀水平板AB长为1.2m,B端靠在光滑竖直墙壁上,板中点C处固连一根长为0.6m的轻质斜杆CO,与板面夹角为53°,O点为固定转轴.在B端放有一质量m=1.6kg静止小木块,先用大小为10N、方向与水平面夹角为53°的拉力F使木块向左滑动,中途撤去拉力F,木块能滑到板的最左端A处,且支架恰好不会失去平衡向逆时针方向翻倒.求:(取g=10m/s2,sin53°=0.8,cos53°=0.6)
如图所示,质量M=1.6kg的均匀水平板AB长为1.2m,B端靠在光滑竖直墙壁上,板中点C处固连一根长为0.6m的轻质斜杆CO,与板面夹角为53°,O点为固定转轴.在B端放有一质量m=1.6kg静止小木块,先用大小为10N、方向与水平面夹角为53°的拉力F使木块向左滑动,中途撤去拉力F,木块能滑到板的最左端A处,且支架恰好不会失去平衡向逆时针方向翻倒.求:(取g=10m/s2,sin53°=0.8,cos53°=0.6)