题目内容
9.一带电量q=6.4×10-19C,质量m=1.6×10-25kg的初速度为零的粒子,经电压U0=200V的加速电场加速后,沿垂直于电场线方向进入E=1.0×103V/m均匀偏转电场.已知粒子在穿越偏转电场过程中沿场强方向的位移为5cm,不计粒子所受重力,求:(1)偏转电场的宽度;
(2)粒子穿越偏转电场后速度的偏转角(用三角函数表示).
分析 带电粒子在加速电场中做匀加速直线运动,根据动能定理求出加速度后的速度,进入偏转电场后做类平抛运动,垂直于场强方向做匀速运动,沿电场方向做匀加速直线运动,根据运动学基本公式即可求解.
解答 解:带电粒子在加速电场中做匀加速直线运动,根据动能定理得:
$\frac{1}{2}$mv02=qU
解得:v0=$\sqrt{\frac{2qU}{m}}$=$\sqrt{\frac{{2×200×6.4×1{0^{-19}}}}{{1.6×1{0^{-25}}}}}=4×1{0^4}m/s$
进入偏转电场后做类平抛运动,则
竖直方向有:a=$\frac{qE}{m}$=$\frac{{1×1{0^3}×6.4×1{0^{-19}}}}{{1.6×1{0^{-25}}}}$=4×109m/s2
y=$\frac{1}{2}$at2=0.05m
解得:t=5×10-6s
所以偏转电场的宽度:l=v0t=4×104×5×10-6=0.2m
垂直于场强方向的速度:vy=at=2×104m/s
所以偏角的正切值为:tanθ=$\frac{{v}_{y}}{{v}_{0}}$=$\frac{1}{2}$
答:(1)偏转电场的宽度为0.2m;
(2)粒子穿越偏转电场过程中偏角的正切值为$\frac{1}{2}$.
点评 注意类平抛运动水平分运动与竖直分运动具有等时性,结合匀速运动与匀变速运动规律解题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4. 如图所示,a,b是某电场中电场线上的两点,将一点点电荷从a移到b,电场力为W,且ab间距离为d,以下说法中正确的是( )
如图所示,a,b是某电场中电场线上的两点,将一点点电荷从a移到b,电场力为W,且ab间距离为d,以下说法中正确的是( )
 如图所示,a,b是某电场中电场线上的两点,将一点点电荷从a移到b,电场力为W,且ab间距离为d,以下说法中正确的是( )
如图所示,a,b是某电场中电场线上的两点,将一点点电荷从a移到b,电场力为W,且ab间距离为d,以下说法中正确的是( )| A. | a,b间的电势差为$\frac{W}{q}$ | B. | a处的电场强度为E=$\frac{W}{qd}$ | ||
| C. | b处的电场强度为E=$\frac{W}{qd}$ | D. | a点的电势为$\frac{W}{q}$ |
4.先后让一价氦离子和二价氦离子以相同的初速度通过同一对平行板形成的偏转电场,进入时速度方向与板面平行,则在离开时一价氦离子和二价氦离子的偏转角的正切之比为( )
| A. | 1:2 | B. | 2:1 | C. | 1:1 | D. | 4:1 |
19.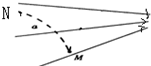 如图所示,实线为已知方向的三条电场线,从电场中M点以一定的速度飞出a个带电粒子,运动轨迹如图中虚线所示.则( )
如图所示,实线为已知方向的三条电场线,从电场中M点以一定的速度飞出a个带电粒子,运动轨迹如图中虚线所示.则( )
 如图所示,实线为已知方向的三条电场线,从电场中M点以一定的速度飞出a个带电粒子,运动轨迹如图中虚线所示.则( )
如图所示,实线为已知方向的三条电场线,从电场中M点以一定的速度飞出a个带电粒子,运动轨迹如图中虚线所示.则( )| A. | a带正电,电场做正功,电势能增加 | B. | a带负电,电场做正功,电势能减少 | ||
| C. | M点的电场比N点弱 | D. | M点的电场比N点强 |
 如图所示,水平放置的传送带以速度v=2m/s向右运行,现将一小物体轻轻地放在传送带A端,物体与传送带间的动摩擦因数μ=0.2,若A端与B端相距4m,求(g取10m/s2)
如图所示,水平放置的传送带以速度v=2m/s向右运行,现将一小物体轻轻地放在传送带A端,物体与传送带间的动摩擦因数μ=0.2,若A端与B端相距4m,求(g取10m/s2)
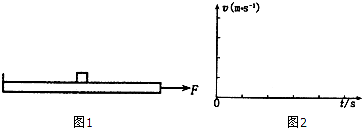 如图1所示,质量为M=2kg,左端带有挡板的长木板放在水平地面上,板上中点处放有一个质量m=1kg的物块,现用一个水平向右大小为7.5N的拉力F拉长木板,物块和长木板间的动摩擦因数为u1=0.1,长木板和水平面之间的动摩擦因数为u2=0.2,运动一段时间后撤去F,最后物块恰好能运动到木板的右端,木板长L=9.6m,物块可视为质点,不计挡板厚度,设最大静摩擦力等于滑动摩擦力,g=10m/s2.
如图1所示,质量为M=2kg,左端带有挡板的长木板放在水平地面上,板上中点处放有一个质量m=1kg的物块,现用一个水平向右大小为7.5N的拉力F拉长木板,物块和长木板间的动摩擦因数为u1=0.1,长木板和水平面之间的动摩擦因数为u2=0.2,运动一段时间后撤去F,最后物块恰好能运动到木板的右端,木板长L=9.6m,物块可视为质点,不计挡板厚度,设最大静摩擦力等于滑动摩擦力,g=10m/s2.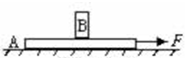 如图所示,质量为M=2kg,长为L=4m的木板A上放置质量为m=1kg的物体B,平放在光滑桌面上,B位于木板中点处,物体B与A之间的动摩擦因数为μ=0.2,B与A间的最大静摩擦力等于滑动摩擦力(B可看作质点,重力加速度g取10m/s2).求:
如图所示,质量为M=2kg,长为L=4m的木板A上放置质量为m=1kg的物体B,平放在光滑桌面上,B位于木板中点处,物体B与A之间的动摩擦因数为μ=0.2,B与A间的最大静摩擦力等于滑动摩擦力(B可看作质点,重力加速度g取10m/s2).求: