Question

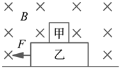
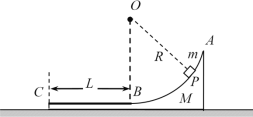
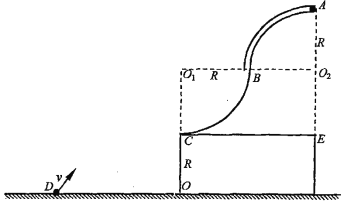
【题目】如图所示，半径均为R的四分之一光滑圆弧轨道AB、BC在B处平滑连接构成轨道ABC,其中AB如为细管道.轨道ABC竖直放置，且固定在水平台阶CE上，圆心连线水平，台阶距离水平地面的高度为R—质量为m的小球静置于水平管口A点，若 小球受微小扰动，从静止开始沿轨道ABC运动，已知小球直径略小于管道内径，重力加速度为g.

(1)小球通过C点时，求轨道对小球的弹力大小；

(2)小球从C点飞出落到地面上，求落地点(图中未画出)到C点的距离S；

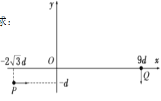
(3)某同学将该小球从地面上的D点斜向右上方抛出，小球恰好从C点水平飞入轨道, 已知水平距离,求小球沿轨道上滑到最高点时离地面的高度h.

Answer 1

【答案】(1)5mg(2)3R(3)2R

【解析】

(1)由到 ，由机械能守恒得：

在点，根据牛顿第二定律可得：

解得：

(2)小球从点做平抛运动，水平方向有：

竖直方向有：

解得：

落地点到点的距离：

S==3R

(3)小球从抛到的过程可以看作由到的平抛运动，设小球到达点的速度大小为，则有：

解得：

设小球从点上滑的最大高度为，对小球上滑到最高的过程，根据动能定理可得：

解得：

所以：